Démonstration par récurrence

[Beignet]

Bonjour,

Je suis Christophe, 53 ans, papa de Blanche qui est en première spé maths. J'ai décidé d'essayer de l'accompagner en maths car elle a besoin d'être accompagnée j'estime ( pas mauvaise mais trop " ado ": nonchalance, tête en l'air, etc... ). J'ai donc pendant tout l'été potassé le livre de 1ere spe maths d'Yvan Monka, je suis en mesure de l'accompagner maintenant pour la première et comme je me suis pris au jeu et que j'aime ça, je suis en train de potasser le livre de terminale. J'ai un niveau BAC +2 Maintenance en 1993 et je suis responsable d'une imprimerie.

Voici le problème:

On considère la suite Un définie pour tout entier naturel n par:

Un+1=Un+4n-6 U0=0

1/ Calculer les termes U1 à U4: simple solution U1=-6 U2=-8 U3=-6 U4=0

2/ Démontrer par récurrence que pour tout entier n on a Un=2n²-8n

Je vous donne la réponse du livre:

Initialisation U0=2x0-8X0=0 Ok initialisé

Hérédité:

Supposons que la propriété soit vraie Uk=2k²-8k
Démontrons que c'est vrai pour k+1
Uk+1=U(k+1)²-8(k+1)=2k²-4k-6

Jusque là ok

Uk+1=Uk+4k-6 ( def de la suite )
Uk+1=2k²-8k+4k-6 par hypothèse de récurrence ( Mouais...., comment arrive t-il là?)
Uk+1=2k²-4k-6 Là il m'a perdu, je n'arrive même pas à dire ce que je ne comprends pas tout se mélange dans ma tête.

QQ'un pourrait-il m'éclairer car j'ai vraiment du mal avec la démarche de démonstartion par récurrence.?

Merci!

Bon we

[Ben314]

Salut,
Le principe de la récurrence, c'est de montrer qu'une certaine propriété dépendant d'un entier est vraie pour un entier "de base" (souvent 0 ou 1), puis que, si elle est vraie pour un entier donné, alors elle est forcément vraie pour l'entier suivant.
Donc, vu que la propriété est vraie pour , elle va être vraie pour le suivant, c'est à dire . Puis, vu qu'elle est vraie pour , elle va être vraie pour , etc et en fait, elle va être vraie pour tout les entiers .
Un exemple concret bébète : tu as devant toi une file de personnes et tu sait que :
- Le premier de la file a un chapeau.
- Toute personne située juste derrière une personne avec un chapeau a elle même un chapeau.
La conclusion, c'est que toutes les personnes de la file ont un chapeau.

Ensuite, concernant ton exo :
- On a donc la propriété "" est vraie lorsque .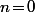
- On suppose que la propriété est vrai pour UN (*) certain entier , c'est à dire que .
On en déduit que . Et, d'un autre coté, on a . Donc on a ce qui signifie bien que la propriété "" est vrai pour l'entier suivant , c'est à dire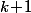

(*) Attention à ne surtout pas écrire (ou sous entendre) qu'on suppose que la propriété est vrai pour TOUT les entiers .

[catamat]

Bonjour
Je venais d'écrire sensiblement la même chose donc je m'abstiens..
Je précise seulement :
Ne pas oublier d'écrire la conclusion "la propriété est donc vraie pour tout entier k"
car le raisonnement par récurrence se fait en 3 étapes : initialisation, hérédité, conclusion)

[Beignet]

Tout d’abord merci de vos réponses. J’ai refait l’exo et ok je comprends mieux le déroulé POUR CET EXO. En revanche j’ai plus de mal sur la méthode par récurrence lorsque je fais d’autres exos je suis perdu.
Qq’un aurait un lien youtube ou autre qui explique clairement la méthode par récurrence svp?

PS: Autant le programme 1ere c’était finger in the noze autant là pour terminale je commence par ça et ça coince. J’espère que la suite sera plus claire

[vam]

Bonjour

Vois un peu cette fiche https://www.ilemaths.net/maths_t_recurrence-cours.php

Le site est complètement gratuit

[Beignet]

Bonjour

Ca y’est je commence à comprendre. Par contre la difficulté selon ce que l’on veut montrer ( multiple de, monotonie d’une suite, etc… ) est de bien partir du bon endroit ( soit de l’hypothèse de récurrence, de k+1 )

[vam]

Ça va venir...le début est déroutant pour tout le monde
Vous pouvez déjà reprendre les exos de la fiche et essayer de les rédiger sans regarder