Démonstration par récurrence

[Fun-e]

Bonjour,
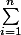
J'ai une démonstration par récurrence à faire mais je bloque complètement : Démontrer pour tout entier naturel n : i^3= (n(n+1))²/4.

J'ai commencé par montré au rang 1 ::
au rang n=1 : i3=1
=1 donc c'est vrai

Supposons que : soit vrai
Alors on aurait :



Quelqu'un pourrait me dire si mon début et juste et m'aider pour la suite? merci d'avance!

[johnjohnjohn]

Bonjour,
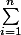
J'ai une démonstration par récurrence à faire mais je bloque complètement : Démontrer pour tout entier naturel n : i^3= (n(n+1))²/4.

J'ai commencé par montré au rang 1 ::
au rang n=1 : i3=1
=1 donc c'est vrai

Supposons que : soit vrai
Alors on aurait :



Quelqu'un pourrait me dire si mon début et juste et m'aider pour la suite? merci d'avance!

Attention aux notations !

Cette notation n'est pas correcte dans le contexte de ton exercice :



Si tu mets ça, plutôt :



je deviens d'accord

De même




Deviennent




A ces détails près , tu es bien parti(e). Je serais toi je continuerais à factoriser ton expression de droite :



je vois bien un n+1 devenir facteur commun

[Fun-e]

Merci pour votre réponse!
Je vais alors rectifier mes erreurs d'écriture.
J'avais déjà essayé de factoriser par (n+1), si je continue ca donne :
et c'est dans la factorisation que je bloque

[johnjohnjohn]

Merci pour votre réponse!
Je vais alors rectifier mes erreurs d'écriture.
J'avais déjà essayé de factoriser par (n+1), si je continue ca donne :
et c'est dans la factorisation que je bloque

Bah non ! Là tu viens de développer !

Repartons de là :





Dans l'expression entre crochets à droite, tu as un n+1 commun aux deux termes de ta somme, tu peux donc FACTORISER !

[Fun-e]

si je factorise par (n+1) on obtient :

Est-ce juste pour l'instant?

[johnjohnjohn]

si je factorise par (n+1) on obtient :

Est-ce juste pour l'instant?

Oui Monsieur ( Madame ) !

Maintenant

=

ça te fait pas penser à un truc ? Genre une identité remarquable ??

[Fun-e]

Si, c'est égal à (n+2)²
Donc on a . Mais ensuite je ne sais pas comment continuer pour montrer que la propriété est vraie

[johnjohnjohn]

Si, c'est égal à (n+2)²
Donc on a . Mais ensuite je ne sais pas comment continuer pour montrer que la propriété est vraie

Pourtant t'as fini !!

(n+1)(n+1) noté autrement, ça donne quoi hein ??

[Fun-e]

Pourtant t'as fini !!

(n+1)(n+1) noté autrement, ça donne quoi hein ??

Euh désolé je dois être nul, mais je comprends pas là! je devrais pas arriver à la fin à ?

[Dinozzo13]

Salut !

Tu suppose que , donc à partir de cette hypothèse, tu dois montrer que , ce que tu viens de faire.

:++:

[Fun-e]

Bonsoir !

Oui, je dois montrer que, sauf que moi j'obtiens ! :triste:

[Dinozzo13]

Si, c'est égal à (n+2)²
Donc on a . Mais ensuite je ne sais pas comment continuer pour montrer que la propriété est vraie

Nam, tu trouves ça :we:
Tu l'as dit plus haut

[Fun-e]

Je suis lent à la détente.... donc ?? excusez-moi si ma question paraît stupide !

[Dinozzo13]

Je suis lent à la détente.... donc ?? excusez-moi si ma question paraît stupide !

Nam, à mon avis, tu as dû mal recopié ce que tu avais écrit.
Je t'ai que tu trouvais plus haut et non pas qui n'est pas du tout la même chose.
Donc reprends le résultat que tu as trovué plus haut :

Le carré ne porte que sur (n+2) et non pas (n+1)(n+2).

[Fun-e]

Nam, à mon avis, tu as dû mal recopié ce que tu avais écrit.
Je t'ai que tu trouvais plus haut et non pas qui n'est pas du tout la même chose.
Donc reprends le résultat que tu as trovué plus haut :

Le carré ne porte que sur (n+2) et non pas (n+1)(n+2).

Ah oui, j'ai fait une erreur de frappe! Donc finalement =?? (si je développe)

[Dinozzo13]

Ah oui, j'ai fait une erreur de frappe! Donc finalement =?? (si je développe)

Oui, c'est ça :+++:

(Si tu factorises, on ne développe rien ici)

[Fun-e]

Oui, c'est ça :+++:

(Si tu factorises, on ne développe rien ici)

Oui mais j'ai développé pour vérifier et je trouve pas la même chose qu'en développant ((n+1)(n+2))² :mur: