Décomposition d'un nombre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par maitre-jiraiya » 17 Aoû 2008, 19:40
par maitre-jiraiya » 17 Aoû 2008, 19:40
Bonjour,
Je cherche à décomposer les nombres du type 2^p en la somme de nombre impaire consécutif.
Pour p paire c'est simple mais pour p impaire c'est autre chose :/
Je voudrais savoir s'il y a une méthode car j'ai beau cherché je bloque.
Merci pour votre aide !
ex :
2^2 = 4 = 1+3
2^3 = 8= 3+5
2^4 = 16 = 1+3+5+7
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 17 Aoû 2008, 19:46
par le_fabien » 17 Aoû 2008, 19:46
........oups j'ai posté une betise :hum:
J'ai une autre idée: par récurrence surement.
 par maitre-jiraiya » 17 Aoû 2008, 19:49
par maitre-jiraiya » 17 Aoû 2008, 19:49
non consécutif^^ 1023 et 1 ne sont pas des nombres impaires consécutifs^^
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 17 Aoû 2008, 19:53
par Euler911 » 17 Aoû 2008, 19:53
Bonjour,
par récurrence surement.
Par récurrence sur quoi? Tu as une formules?!
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 17 Aoû 2008, 19:59
par le_fabien » 17 Aoû 2008, 19:59
Euler911 a écrit:Bonjour,
Par récurrence sur quoi? Tu as une formules?!
Bien sur que j'ai une formule!
J'essaie de le démontrer.
Je n'ai pas trouvé de somme pour 2^51.
Il me semble que ce ne sera pas possible.
Et toi Euler911 tu as trouvé quelquechose ? :we:
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 17 Aoû 2008, 20:01
par Euler911 » 17 Aoû 2008, 20:01
LEFAB11 a écrit:Bien sur que j'ai une formule!
:
Peux-tu nous la donner?
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 17 Aoû 2008, 20:10
par le_fabien » 17 Aoû 2008, 20:10
Non car c'était une mauvaise voie.
soit une puissance de 2: 2^n avec n entier impair
2^(n-1) étant pair est somme de deux nombres entiers égaux soit:
2^(n-1)=m+m
donc 2^n=2m+2m=(2m-1) + (2m+1)
Conclusion ...

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 17 Aoû 2008, 20:43
par nuage » 17 Aoû 2008, 20:43
Salut,
LEFAB11 a écrit:Bien sur que j'ai une formule!
J'essaie de le démontrer.
Je n'ai pas trouvé de somme pour 2^51.
Il me semble que ce ne sera pas possible.
Et toi Euler911 tu as trouvé quelquechose ? :we:

-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 17 Aoû 2008, 20:47
par le_fabien » 17 Aoû 2008, 20:47
J'avais choisis 51 au pif. :ruse:

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 17 Aoû 2008, 20:48
par nuage » 17 Aoû 2008, 20:48
Et il me semble que l'on peut induire la formule de ma réponse.
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 20:58
par magnolia86 » 17 Aoû 2008, 20:58
On veut écrire
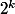
comme somme d'entiers impairs consécutifs.
C'est possible : on a même le choix
Soit deux entiers i,j tels que
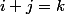
avec
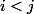
On pose

et

On a alors
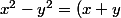.(x-y) = 2^j . 2^i = 2^k)
Or
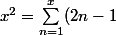)
et
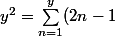)
donc
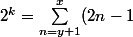)
.
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 21:08
par magnolia86 » 17 Aoû 2008, 21:08
Ok, c'est juste.
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 21:10
par magnolia86 » 17 Aoû 2008, 21:10
ok, c'est juste.
 par maitre-jiraiya » 17 Aoû 2008, 21:10
par maitre-jiraiya » 17 Aoû 2008, 21:10
merci pour ces éclaircissement, surtout nuage, ça a pu m'aider à faire une formule géneral pour p impaire.
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 21:12
par magnolia86 » 17 Aoû 2008, 21:12
maitre-jiraiya a écrit:merci pour ces éclaircissement, surtout nuage, ça a pu m'aider à faire une formule géneral pour p impaire.
nul besoin de supposer p impair. En plus, on a le choix dans l'intervalle de sommation :
Pour deux entiers i,j tels que
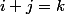
avec
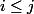
alors
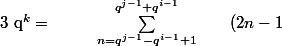)
.
 par maitre-jiraiya » 17 Aoû 2008, 21:15
par maitre-jiraiya » 17 Aoû 2008, 21:15
j'ai vérifier ma formule sa ma l'air bon :
}2}^{\frac{n^p(n+1)}2 -1} 2i+1=n^{2p+1})

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 17 Aoû 2008, 21:19
par nuage » 17 Aoû 2008, 21:19
[CENTER] :++: :++: :++: Bravo :++: :++: :++:[/CENTER]
C'est une belle démonstration !
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 21:20
par magnolia86 » 17 Aoû 2008, 21:20
maitre-jiraiya a écrit:j'ai vérifier ma formule sa ma l'air bon :
}2}^{\frac{n^p(n+1)}2 -1} 2i+1=n^{2p+1})
oui, je crois que cette formule est correcte également.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 163 invités
