Croissance (ou décroissance)

[Quidam]

Bonjour à tous,

Je cherche une confirmation.

Une fonction est strictement croissante sur un intervalle si x1
Je ne suis pas certain que la définition de la croissance soit étendue à tout ensemble : chaque fois que l'on fait référence au sens de variation d'une fonction, c'est toujours "sur un intervalle".

C'est-à-dire : Peut-on dire qu'une fonction est croissante sur son domaine de définition (même s'il ne s'agit pas d'un intervalle) si x1
Mais même si cela est possible, il me semble au contraire que bien que la dérivée de 1/x soit négative en tout point de son ensemble de définition, il serait tout à fait incorrect de prétendre que la fonction 1/x est décroissante sur son domaine de définition, même si l'on admettait l'extension ci-dessus de la définition.

Est-ce que quelqu'un peut me confirmer ce point ?
Merci d'avance !

[xyz1975]

Non, la monotonie, la dérivation sont des notions très liées à la notion de connexité (ie aux intervalles).

Un simple exemple si on considère la fonction elle est définie sur qui est réunion de 2 intervalles mais on ne peux pas dire qu'elle est croissante sur sinon :



Soit qui est faux.

Ceci est dû au fait qu'on a pris deux réels dans deux intervalles différents.

[Quidam]

Merci de ta réponse.

Mais cela ne répond que partiellement à ma question.

Peut-on dire qu'une fonction est croissante sur son domaine de définition (même s'il ne s'agit pas d'un intervalle) si x1<x2 entraîne f(x1)<f(x2) pour tout couple de valeurs x1 et x2 de son domaine de définition ?

Non !

Ça c'est clair !

, la monotonie, la dérivation sont des notions très liées à la notion de connexité (ie aux intervalles).

Cela l'est beaucoup moins. J'ai du mal à évaluer la valeur d'une expression comme "assez liées" ou "très liées".

J'attendais donc une réponse comme "Oui, on peut définir la croissance sur un domaine qui ne soit pas un intervalle", ou au contraire, "Non, il n'en est pas question ! A aucun moment on ne définit la croissance sur un ensemble autre qu'un intervalle"

Quant à ton exemple (qui au demeurant est exactement le même que le mien au signe près), même s'il se faisait de définir la croissance au sens large que j'ai évoqué, il est clair que 1/x ou -1/x n'y répondrait pas, pour la raison que tu as explicitée !

Cependant, on peut bien imaginer une fonction définie sur * par f(x)=x pour tout x non nul et f(0) non défini. Alors la définition que j'évoquais serait utilisable et on pourrait dire que f est croissante sur son domaine de définition au sens large.

Donc la réponse que j'attendais est "Non ! Même dans ce cas-là on ne pourra pas dire que la fonction est croissante sur son ensemble de définition" (c'est ce que je crois en fait, mais je souhaitais une confirmation)

Merci de ton intervention en tous cas !

[Nightmare]

Salut !

Je ne suis pas d'accord avec xyz1975, tu dis qu'on ne peut pas étendre la notion de monotonie à un ensemble non connexe et tu justifies avec l'exemple de la fonction inverse qui est décroissantes sur les composantes connexes de R* mais pas sur R* lui même. Nous sommes d'accord sur ce point, mais ce n'est pas la question de Quidam qui demande de savoir si l'on peut appeler "monotone" une fonction qui vérifie les conditions de monotonies sur un ensemble quelconque.

Pour moi, la réponse est oui et la fonction inverse n'est pas un contre exemple puisqu'elle ne vérifie pas cette propriété.

Si on prend une fonction quelconque qui décroisant disons sur R-, qui fait n'importe quoi sur [0,10] puis qui décroit sur [10,+oo[ de sorte que f(10) < f(0) alors on a bien une fonction décroissante sur R\[0,10]

[Switch87]

Salut!
La question est intéressante.
D'après ce que je viens de lire sur internet, la notion de monotonie sur un ensemble qui n'est pas un intervalle existe, mais elle est très peu utilisée. Elle est la même que sur un intervalle: pour une fonction strictement croissante, x1 f(x1)Du coup, -1/x est bien croissante sur R-* et sur R+*, mais pas sur R*.

[xyz1975]

Nightmare: Je pense que le théorème ainsi que sa démonstration sont clairs, je vois pas comment tu pourras affirmer la croissance d'une fonction f sur un ensemble autre qu'un intervalle. L'exemple que tu donnes ne peut pas générer une définition de la monotonie d'une fonction sur un ensemble quelconque.

[xyz1975]

Salut !

mais ce n'est pas la question de Quidam qui demande de savoir si l'on peut appeler "monotone" une fonction qui vérifie les conditions de monotonies sur un ensemble quelconque.

Pour moi, la réponse est oui et la fonction inverse n'est pas un contre exemple puisqu'elle ne vérifie pas cette propriété.

Je dirai encore non! donnes moi une condition suffisante (raisonnable) pour qu'une fonction soit monotone sur une réunion de plusieurs intervalles.

La même chose pour une dérivée nulle sur un ensemble quelconque.

[Nightmare]

Je ne comprends pas ce qui te gène, pourquoi vouloir borner la notion de monotonie à un intervalle?

Pour moi l'étendre à un ensemble quelconque est clair avec l'exemple que j'ai donné. Une fonction est croissante sur un ensemble si on peut ordonner les images de la même façon que les éléments, à partir de là on s'en fiche qu'il y ait connexité ou non.

Je prends un exemple courant, on regarde les prix d'un produit boursier imaginaire qui se comporte de telle façon que de 1990 à 2000 son prix a augmenté, de 2000 à 2003 il subit une faible fluctuation de sorte qu'en 2003 le prix soit le même qu'en 2000 et ce 2003 à aujourd'hui il augmente. On a bien le droit de dire que le prix est croissant depuis 20 ans sauf sur [2000,2003] non?

Une condition pour moi suffisante de croissante sur [a,b]U[c,d] est que la fonction doit être croissante sur [a,b] et sur [c,d] et que f(c) > f(b).

Cela te convient-il ?

[Quidam]

Nightmare: Je pense que le théorème ainsi que sa démonstration sont clairs, je vois pas comment tu pourras affirmer la croissance d'une fonction f sur un ensemble autre qu'un intervalle.

xyz1975 : Nightmare n’affirme rien du tout ! Il se contente de répondre à ma question : et se prononce pour l'avis contraire au tien. Apparemment, les avis sont partagés, mais indépendamment de cela, Nightmare ne voit pas (tout comme moi) d’objection à une possible extension de la définition. Merci à Nightmare d'apporter un contrepoids.

La question que j’ai posée me tarabuste depuis un moment ; comme je l’ai dit plus haut, dans les livres que je fréquente actuellement (ceux du lycée, d’où le choix du forum lycée), chaque fois que l’on définit la croissance (resp. la décroissance) d’une fonction, on la définit toujours sur un intervalle. La question se pose pour les lycéens principalement sur la fonction harmonique (). 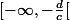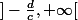Il est clair pour tous que la fonction est soit croissante sur chacun des deux intervalles et , soit décroissante sur chacun de ces deux intervalles. Et nombre de lycéens font l’erreur de déclarer que la fonction est croissante « sur son ensemble de définition », ce qui est manifestement faux. Le fait qu’elle soit croissante (resp. décroissante) sur tout intervalle inclus dans son ensemble de définition n’autorise pas à dire qu’elle est croissante (resp. décroissante) sur son ensemble de définition.

Il résulte du fait que quasiment aucune fonction étudiée au lycée ne pourrait satisfaire la définition que j’ai évoquée, que j’ignore justement si cette définition élargie n’existe pas et n’est pas utilisée. (je dis quasiment uniquement par sécurité !)

A cet égard, je remercie d’ailleurs également Switch87 d’apporter sa contribution.

D'après ce que je viens de lire sur internet, la notion de monotonie sur un ensemble qui n'est pas un intervalle existe, mais elle est très peu utilisée. Elle est la même que sur un intervalle: pour une fonction strictement croissante, x1 f(x1)<f(x2).

Au passage, Switch87, je suppose que tu voulais dire « croissante » et non « décroissante » !

Du coup, -1/x est bien décroissante sur R-* et sur R+*, mais pas sur R*.

Mais pour revenir à xyz1975, je ne vois pas à quel théorème et à quelle démonstration tu fais allusion. Il ne s’agit nullement ici de la démonstration d’un théorème, mais tout simplement d’une définition. Soit elle existe, soit elle n’existe pas ! C’était simplement l’objet de ma question naïve…

[Switch87]

oui oui, c'est une coquille ;)

[busard_des_roseaux]

Pour une fois je ne suivrai pas NightMare..

Il est important que le domaine de définition soit un intervalle (partie connexe)
sinon, l'exemple de la fonction inverse montre que l'on ne peut pas passer
de la stricte croissance locale (partout) de à la croissance sur l'ensemble du domaine de définition, ce qui est quand même ennuyeux.

[Nightmare]

Je vous avoue que j'ai beaucoup de mal à comprendre vos points de vue.

La notion de monotonie veut juste dire que si on a un ordre sur nos éléments, la fonction va conserver (ou inverser) cet ordre, où est la notion de connexité ici?

En outre, je crois qu'on aura tous parlé de suite croissante ou décroissante, une suite n'étant rien d'autre qu'une fonction de N dans R. Ici, il est totalement licite de dire que la fonction x->x² est croissante sur N non?

Pour finir, voici un paragraphe intéressant de mon cours de L2 (structures discrètes) :

Soit (E,) un ensemble ordonné. On dit qu'une fonction est croissante (resp. décroissante) si :
, (resp. )

Là encore la définition est globale, pour parler de monotonie on a besoin d'un ensemble, d'un ordre et d'une fonction, pas besoin de connexité.

busard_des_roseaux > Tu parles du problème pour passer de la croissance locale à la croissance globale. Pour moi ce n'est pas un problème, c'est même naturel puisque la monotonie(à la différence de la continuité et de la dérivabilité) n'est pas un phénomène local.