Correction petit exercie (combinaison) [résolu]

[Abuj]

Bonsoir,

Pouvez-vous me dire si c'est bon ou pas.

1)
Enoncer: De combien de manières différentes puis-je répartir 7 pièces de monnaie toutes différentes
entre ma poche gauche et ma poche droite ?

Voici mon raisonnement:


2) Que signifie l'abréviation C pn
J'ai dis que c'était une preuve par récurrence ?

3) Comment calcules-ton C pn
Moi j'ai mis la formule c'est bien ça ?


Merci

[bolza]

Bonjour,

1) attention, ce que tu as calculé c'est le nombre de façons de choisir 2 pièces parmi 7.
ce qui est très différent du "nombre de façons de répartir 7 pièces dans 2 poches" !!!
Indication : tu peux avoir 1 pièce dans une poche et 6 dans l'autre, ou alors 2 dans une poche et
5 dans l'autre, etc.

2) d'après ce que tu as répondu à la question 3) "C pn" à l'air d'être un nombre...
Or ici tu dit que c'est un raisonnement par récurrence...
Est-tu conscient que ta réponse à la question 2) est un non-sens ?
En fait ici on te demande à quoi correspond le nombre que tu as donner à la question 3)

3) Si j'ai bien interprété ton "C pn" alors oui, c'est bien ça ^^

[Lostounet]

Ils disent que les pièces sont toutes différentes.
Cela veut dire que par exemple si on les note
A B C D E F G

Avoir A dans droite ou B dans droite c'est pas pareil non.
Je dirais 2 choix pour chacune des 7 pièces ce qui totalise 128 choix possibles.

En plus c'est la somme des coefficients binomiaux: on compte combien de groupes de 1 pièce on peut faire, puis groupes de 2..

Soit tu as dans la poche droite:
* rien 1
* A ou B ou C ou D.. 1 parmi 7
* AB AC ou CD etc 2 parmi 7


Après j'ai un doute

[Abuj]

Bonsoir,

Merci pour vos réponses, bhein visiblement je me suis complétement gouré alors ?
@Lostounet: comment tu as fais pour trouver la réponse ? J'ai rien compris moi alors...

[MABYA]

Ce ne sont pas des arrangements ni des combinaisons, en fait pour 7 pièces inutile d'aller dans la théorie combinatoire.
G-- D
1---6
2---5
3......4
4......3
5......2
Je ne vois que 5 possibilités (que ce soit dans la gauche ou la droite c'est effectivement la même chose

[Abuj]

Bonsoir,

Ton raisonnement est bon. Cependant je pense qu'il y a 6 possibilité.

G--D
6---1
1---6
2---5
3......4
4......3
5......2

[beagle]

Ce ne sont pas des arrangements ni des combinaisons, en fait pour 7 pièces inutile d'aller dans la théorie combinatoire.
G-- D
1---6
2---5
3......4
4......3
5......2
Je ne vois que 5 possibilités (que ce soit dans la gauche ou la droite c'est effectivement la même chose

un petit coup de fatigue?
0-7, 6-1, 7-0
maintenant , ben non c'est pas bon puisque les pièces sont toutes différentes.

[bolza]

En fait non :
d'abord il manque les cas 0-7 ; 6-1 ; et 7-0.
ensuite les pièces sont discernable, c'est à dire que pour le cas 2-5 par exemple,
avoir les pièces A et B dans la poche gauche et C,D,E,F,G dans la poche droite, ce n'est pas le même
cas que avoir F et G dans la poche gauche et A,B,C,D,E dans la poche droite.

Donc pour le cas 2-5 pour savoir combien il y a de possibilité c'est simple :
je choisis 2 pièces parmi 7 , je les mais dans ma poche gauche, et les autres, je les mets
dans ma poche droite. Donc j'ai C(2,7) cas possible pour le cas 2-5.
après quand on somme tous les cas on retombe sur le résultat trouvé par Lostounet.
(On retrouve un résultat bien connu sur les coefficients binomiaux).

@Abuj : en fait les C(p,n) ce sont le nombre de façon de choisir p éléments parmi n
c'est en fait ce qui t'est demandé à la question 2)
vois tu pourquoi ce nombre est égal à la formule que tu as donné à la quetion 3) ?

[Abuj]

Bonsoir Bolza,

J'ai compris merci beaucoup !

Je viens d'additionner j'arrive bien à 128
j'ai 1 + 7 + 21 + 35 + 35+ 21 + 7 + 1

Merci encore les gas !

[Ben314]

Salut,
Perso,. j'aurais tendance à penser que, d'additionner les coeff. binomiaux, c'était pas la réponse attendu à la question, mais peut-être que je me trompe...
Moi, j'aurais répondu avec un arbre :
- Première "branche" avec deux choix : soit on met la pièce A à droite, soit on la met à gauche.
- Au bout de chacun des deux choix précédents, deux nouveau choix : soit on met la pièce B à droite, soit on la met à gauche.
- Etc jusqu'à arriver à la pièce G.

Le but étant assez clairement de pas tracer tout l'arbre, mais de rapidement voir combien il y a de possibilités pour k pièces (à savoir )

[MABYA]

effectivement @abuj, il y en a bien 6
1et 6
et
6 et 1
pour 0 et 7 et 7 et 0, je ne suis pas d'accord, ce serait fermer une poche

[Pseuda]

Bonjour,

Les pièces sont toutes différentes : il faut les appeler par exemple, P1, P2, .... P7.

Chacune de ces pièces peut être dans la poche gauche, ou non (et si elle n'est pas dans la poche gauche, elle est forcément dans la poche droite). Et les pièces sont disposées dans les poches de manière indépendante.

Il y a 2 façons possibles de disposer chaque pièce (poche gauche ou poche droite). Donc le nombre de façons de disposer ces 7 pièces dans 2 poches est : 2x2x2x2x2x2x2 = 2^7.

Si ces pièces étaient identiques, il n'y aurait en effet que 8 façons de les disposer (en comptant le 0 et le7), mais dans ce cas, on perdrait l'équiprobabilité. Il faudrait d'abord les considérer différentes pour pouvoir calculer plus facilement les probabilités (mais ce n'est pas demandé).

[bolza]

Salut,
Perso,. j'aurais tendance à penser que, d'additionner les coeff. binomiaux, c'était pas la réponse attendu à la question, mais peut-être que je me trompe...
Moi, j'aurais répondu avec un arbre :
- Première "branche" avec deux choix : soit on met la pièce A à droite, soit on la met à gauche.
- Au bout de chacun des deux choix précédents, deux nouveau choix : soit on met la pièce B à droite, soit on la met à gauche.
- Etc jusqu'à arriver à la pièce G.

Le but étant assez clairement de pas tracer tout l'arbre, mais de rapidement voir combien il y a de possibilités pour k pièces (à savoir )

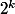
Peut-être, je ne sais pas ^^
Le fait qu'on introduit les coefficients binomiaux aux deux questions suivantes m'a fait pensé
qu'il fallait les utiliser. Mais justement le fait qu'il y ait ces deux façon de compter illustre bien
que la somme des coefficients binomiaux "d'une même ligne" est une puissance de 2.

On peut même aller plus loin : si au lieu d'avoir deux poches, on avait deux boîtes.
et que dans la première boîte il y a a compartiments et dans la deuxième il y a b compartiments.
de combien de façon peut-on répartir les pièces dans les deux boites ?

façon de compter n°1 : il y a (a+b) compartiment, donc pour chaque pièce on a (a+b) choix
on trouve donc (a+b)^7

façon de compter n°2 : comme précédemment sauf que là pour le cas 2-5 par exemple
on a toujours C(2,7) cas possible, mais cette fois pour répartir les 2 pièces dans la première
boîtes on a a choix pour chacune des deux pièces, ce qui fait a² choix possible.
et pour les 5 autre pièces dans l'autre boîte on de même b^5 choix possible.
Ce qui fait donc au total pour le cas C(2,7)*a²*b^5.
En sommant ainsi tous les cas, on retrouve la formule du binôme du Newton.

Finalement avec quelque pièces et deux boîtes, on pourrait faire un bon petit dm ^^