Coordonnée d'un point dans un triangle

[Anonyme]

Voila mon problème, j'ai un triangle rectangle d'angle A, B et C.
Les coordonnées de A et de B sont connues.
La distance AC est = d.

Ma question, comment déterminer les coordonnées de C?

Cordialement

PS: Un shéma plus parlant est présent ici=
http://img120.imageshack.us/my.php?image=triangle8wy.jpg

[sbz]

sur ton dessin, on a C(x3; y3) qu'est ce que tu veux de plus? ta pas non plus les coordonnées de A et B , je vois pas le pb......

[lasaid]

salut ,
je crois que vous devez tracer le repere celà va nous faciliter la tache

[mathador]

Salut
Le réflexe que j'ai (qui n'est peut-être pas bon ici) : orthogonalité ? PRODUIT SCALAIRE !!!

ET l'indication de longueur qui est donnée
Il rest à développer/réduire, et résoudre ...
De toute façon, pour un cas donné, on aura toujours 2 possibilités : deux points symétriques par rapport à la droite. A voir ...

[Chimerade]

Voila mon problème, j'ai un triangle rectangle d'angle A, B et C.
Les coordonnées de A et de B sont connues.
La distance AC est = d.

Ma question, comment déterminer les coordonnées de C?

C appartient au cercle de diamètre AB ; son équation est ce qu'a dit mathador (sauf que Mathador a supposé que le triangle était rectangle en A alors que c'est en C, mais tout le monde avait compris) :
(X-x1)*(X-x2)+(Y-y1)*(Y-y2)=0

Comme la distance AC est d, C appartient également au cercle de centre A et de rayon d :

(X-x1)^2+(Y-y1)^2-d^2=0

YAPUKA résoudre : tu obtiendras deux points symétriques par rapport à AB.

[Anonyme]

Je vous remercie pour vos réponse, mais n'existe t'il pas une méthode de résolution trigonométrique?

[Chimerade]

Je vous remercie pour vos réponse, mais n'existe t'il pas une méthode de résolution trigonométrique?

Si, bien sûr ! Tu peux déterminer l'angle par son cosinus :
Tu connais AC=d, et tu peux calculer AB :



Enfin :

Ensuite, tu vas déterminer un vecteur D parallèle à AB et de norme d. Les coordonnées de D seront :


et


Enfin il te resteras à faire tourner le vecteur D d'un angle ou et à ajouter le résultat aux coordonnées de A :




pour l'un des deux points, et :




pour le deuxième. Après, c'est à toi de choisir celui qui t'intéresse...

[mathador]

je me permets une remarque sur l'utilisation de LaTeX : contrairement à la plupart des logiciels, la commande de multiplication n'est pas * mais : \times .
Ca ne change pas grand chose, simplement d'afficher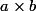 au lieu de ... simple précision donc !

[celge]

Excuse moi chimerade, mais je n'ai pas tres bien compris le calcul des coordonnées de D (le vecteur D) .(pourquoi multiplier par d ?) Je dois etre fatigué, non ? ;) (ou je n'ai pas tout suivi peut etre)

[celge]

Pardon, j'ai compris, c'est parce que tu le prends à partir de A; pour avoir AC, c'est ca ?

[Chimerade]

je me permets une remarque sur l'utilisation de LaTeX : contrairement à la plupart des logiciels, la commande de multiplication n'est pas * mais : \times .
Ca ne change pas grand chose, simplement d'afficher au lieu de ... simple précision donc !

Merci mathador ! Comme je l'ai dit plus tôt (dans un autre post), j'apprends les choses une à la fois, lorsque j'en ai absolument besoin, ce qui n'était pas le cas de *.
Donc, désormais, j'utiliserai \times...

[Chimerade]

Pardon, j'ai compris, c'est parce que tu le prends à partir de A; pour avoir AC, c'est ca ?

Oui, c'est cela !