Conjecturer l'expression de u(n) en fonct° de n et démontrer

[Willxxx]

Bonjour,
Voilà, j'ai un exercice à faire et je galère pas mal. J'apprécierais que vous m'aidiez à trouver la bonne voie.
L'énoncé c'est: la suite u(n) est définie par u0=3 et pour tout entier naturel n, u(n+1)= -u(n)+4.
Ils demandaient d'abord de déterminer les 5 premiers termes puis de conjecturer et de démontrer.
Voilà ce que j'ai trouvé:
u1=1
u2=3
u3=1
u4=3
u5=1
Et c'est là que ça coince... je ne vois pas comment conjectuer u(n) en fonction de n alors que je ne vois pas e rapport, il n'y a que deux résultats possibles.
Merci de votre aide!!

[Pseuda]

Bonjour,

Donc si n est pair = ?
et si n est impair = ?

Ceci est une conjecture.

Il faut ensuite la démontrer.

[chan79]

Ceci est une conjecture.

Il faut ensuite la démontrer.

salut
Par récurrence, éventuellement

[Razes]

Je peux te donner la réponse tout de suite mais je te propose plutôt de cherche une suite géométrique , tel que 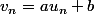; cherche et ainsi tu peux déterminer et par de suite .