[Arithmétique] Congruence et équation de pythagore
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par GhandiIsGood » 23 Oct 2010, 14:57
par GhandiIsGood » 23 Oct 2010, 14:57
Bonjour,
Je suis tombé sur l'exercice suivant et je ne sait pas du tout comment le résoudre.
En étudiant les congruences modulo 5, vous devrez démonter que si les entiers a,b et c vérifient
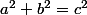
alors l'un au moins est divisible par 5.
Alors si vous avez une astuce, je suis preneur. D'ailleurs je ne sait pas ce que veut dire étudier les congruences modulo 5, auriez vous aussi une info là dessus.
Merci bien.
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 23 Oct 2010, 15:26
par Mortelune » 23 Oct 2010, 15:26
Bonjour, as-tu déjà fait un tableau avec les congruences et les puissances ? c'est une méthode exhaustive donc un peu bourrine mais en modulo 5 on s'en sort rapidement.
Exemple avec les modulo 3 :
à la puissance 1 : 0 - 1 - 2 [3]
à la puissance 2 : 0 - 1 - 1 [3]
 par GhandiIsGood » 23 Oct 2010, 15:58
par GhandiIsGood » 23 Oct 2010, 15:58
Merci pour l'info, Cela me dit quelque chose,
si on fait
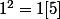
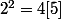
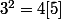
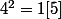
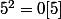
et ainsi de suite...
Je me suis dit que cela serait une bonne idée de faire un tableau avec les congruences modulo 5 de la somme des carrés mais je vois pas comment exploiter, pourtant je "sens" quelque choses.
Mais meme avec cela je n'arrive pas à relier au problème. Pas facile l'arithmétique il faut dire :mur:
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 23 Oct 2010, 16:11
par Mortelune » 23 Oct 2010, 16:11
Oui c'est ça, fin pour ton tableau tu peux t'arrêter à 4 du coup.
On a donc le choix pour combiner 0,1 et 4 en en sommant 2 pour obtenir un 3e le tout modulo 5. Ce qui donne 6 additions possibles.
Et à chaque fois que l'égalité est vérifiable on voit un apparaitre un 0, donc un multiple de 5.
 par GhandiIsGood » 23 Oct 2010, 16:39
par GhandiIsGood » 23 Oct 2010, 16:39
Oki, mais ce raisonnement est il valable, n'y a t'il pas une méthode plus arithmétique pour y arriver, avec une démo bien léchée? Car la même si cela marche j'ai l'impression que c'est du bricolage.
Ceci dit dans mon tableau j'ai des cas qui comme on peut s'y attendre ne sont pas divisibles par 5 (pas de zero), comment les écarter car on ne tombe pas sur qqchose de la forme
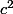
?
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 23 Oct 2010, 17:30
par Mortelune » 23 Oct 2010, 17:30
ça revient à un traitement par cas donc la démonstration est correcte pour quelque chose de plus léché je n'ai pas d'idée.
Mais modulo 5 tu as donc les cas suivant pour
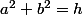
0+0=0
0+1=1
0+4=4
1+1=2 (impossible car dans ce cas h ne peut être un carré d'après le résultat précédent)
1+4=0
4+4=3 (idem que pour 1+1)
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 23 Oct 2010, 17:51
par nodjim » 23 Oct 2010, 17:51
C'est encore plus visible si on remplace 4 par (-1).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
