Complexes : question tordue

[_-Gaara-_]

Salut à tous ,

alors voilà je me suis dit que vu qu'il existe r*exp(ix) pour représenter n'importe quel complexe, il pourrait exister la même chose mais en ln(x) du genre : ln(r) + ln(ix) ????

Je sais que pour les valeurs négatives ça ne marchera pas mais je trouve ça bizarre :hein: :hein:

[skilveg]

En fait, ce n'est ni tordu ni bizarre! :we: (Si ce n'est qu'on poserait plutôt )

Alors: oui, on peut définir un logarithme sur privé d'une droite qui va en plus être continu (plus précisément, il existe des logarithmes holomorphes sur tout ouvert simplement connexe ne contenant pas zéro, mais je ne sais pas si ça te parle...).

Ton logarithme est défini sur . Des fois, il est utile d'en définir sur d'autres domaines de , selon le problème que l'on se pose.

[_-Gaara-_]

xD merci ^^

en fait j'ai fait une énorme erreur pour l'exponentielle mais bon ^^

(plus précisément, il existe des logarithmes holomorphes sur tout ouvert simplement connexe ne contenant pas zéro, mais je ne sais pas si ça te parle...)

J'en ai entendu parler lors d'une conférence mais je n'ai pas tout capté

Mais aurais-tu un exemple de problème où l'utilisation de ce logarithme est nécessaire ?

Conserve-t-il les mêmes propriétés que le log naturel défini sut R*+ ?

En tout cas merci ^^

[skilveg]

Il me semble que c'est surtout un résultat technique qui aide à démontrer des théorèmes... Mais sinon, ça permet de montrer que certaines fonctions de la variable complexe sont des exponentielles d'autres fonctions ou qu'elles admettent des racines -ièmes.

`A part ça, ça peut aussi servir à calculer des intégrales (par le théorème des résidus), par exemple
[CENTER] et [/CENTER]

En théorie spectrale, ça permet de montrer que certains éléments d'une algèbre de Banach commutative sont des exponentielles...

Pour ce qui est des propriétés algébriques, je dirais que celles du logarithme réel usuel sont conservées tant que l'on n'a pas de problèmes d'argument (par exemple, si sont dans , il peut arriver que n'y soit pas; du coup n'est pas forcément défini même si 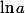et le sont).

Edit: au passage, je viens de remarquer que c'est en définissant de bons logarithmes qu'on arrive à justifier ceci: si vérifie , alors on peut écrire ; et si en plus vérifie certaines conditions de régularité, alors 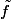aussi.

[_-Gaara-_]

Merci beaucoup skilveig !! :we:

Je comprends pas trop la dernière partie du message mais je m'y pencherais dès ce soir ! je dois essayer de comprendre =)

et sinon j'essayerais de calculer les intégrales ^^ :id:

Merci encore =)

[skilveg]

Pas de quoi ! :jap:

Si tu trouves un moyen de calculer ces intégrales sans variable complexe, dis-le-moi, ça m'intéresse!

Bonne soirée

[_-Gaara-_]

Pas de quoi ! :jap:

Si tu trouves un moyen de calculer ces intégrales sans variable complexe, dis-le-moi, ça m'intéresse!

Bonne soirée

xD je n'ai pas trouvé les intégrales c'est trop dur <_< mais je n'abandonne pas :we:

[Weensie]

Je trouve que la question est extrêmement interessante , et la réponse de skilveg est absoluement complète .
Je serais vraiment curieux de deduire les propriétés des bijections reciproques des fonctions holomorphes telles que l'exponentielle complexe.
Quand je parle de propriétés je ne parle pas uniquement de leur définition sur un ensemble mais aussi de leur porporétés trgonométriques :)
Ceci dit ca m'a lir faisable , je m'y penche et je vous dis