Bonjour,
Vous connaissez sans doute l'exo du château de cartes où il faut trouver une formule générale pour le nombre de cartes en fonction du nombre d'étages.
Soit (u_n) la suite donnant le nombre de cartes et n le nombre d'étages. J'ai conjecturé u_n=(n(3n+1))/2 en calculant le nombre de cartes pour les premiers étages. Maintenant pour m'assurer que la conjecture est exacte, il suffit que je la montre par récurrence. Mais pour l'hérédité c'est un peu compliqué car que dire de u_n+1 ? Je ne dispose que d'une seule formule de (u_n). J'ai pensé à établir une formule par reccurence de u_n+1 en fonction de u_n mais il faudrait aussi que je montre cette formule avant de pouvoir l'utiliser... Donc doit-on admettre la validité de la formule ?
Merci bien.
Château de cartes.
12 messages
- Page 1 sur 1
Re: Château de cartes.
Oublie le contexte du château de cartes.
Explique la démarche que tu connais pour une démonstration par récurrence. J'ai l'impression que c'est le principe même de démonstration par récurrence qui n'est pas compris.
Explique la démarche que tu connais pour une démonstration par récurrence. J'ai l'impression que c'est le principe même de démonstration par récurrence qui n'est pas compris.
Re: Château de cartes.
Si je connais parfaitement le principe de reccurence, simple, double forte. Ce que je dis c'est que la formule conjecturee doit être montrée par reccurence non ?. Pour l'hérédité, comment on s'y prendrai ? On part de u_n+1 mais ensuite ?
Re: Château de cartes.
Bonjour,
Un peu de réflexion te dira combien de cartes ajouter à un chateau de cartes à n étages pour obtenir un château de cartes à n+1 étages : il y a les cartes obliques qui vont par deux (combien ?), et les cartes horizontales qui séparent les étages (combien ?).
Un peu de réflexion te dira combien de cartes ajouter à un chateau de cartes à n étages pour obtenir un château de cartes à n+1 étages : il y a les cartes obliques qui vont par deux (combien ?), et les cartes horizontales qui séparent les étages (combien ?).
Re: Château de cartes.
Bah oui évidemment. Cela revient en fait à déterminer l'expression de (u_n) par récurrence donc u_n+1 en fonction de u_n. Mais ce que je me dis c'est est-ce qu'on trouve cette formule, on l'utilise dans l'hérédité et c'est OK, ou est ce qu'on conjecture cette formule, on la démontre par reccurence avant de l'utiliser dans l'hérédité. Vous voyez ? Dans tous les cas il y a une formule qu'on trouve mais qu'on ne démontre pas.
Re: Château de cartes.
Tu te fais une drôle d'idée de ce qu'est une démonstration en combinatoire.
Pour moi quand je compte le nombre de cartes qu'il faut ajouter à un château à étages pour obtenir un château à
étages pour obtenir un château à  étages, c'est une démonstration tout à fait valable.
étages, c'est une démonstration tout à fait valable.
Et une fois que j'ai ainsi en fonction de
en fonction de  et de
et de  , il suffit de partir de
, il suffit de partir de 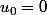 pour établir par récurrence une formule close pour
pour établir par récurrence une formule close pour  . On a bien une démonstration de cette formule close.
. On a bien une démonstration de cette formule close.
Alors finalement, où est le problème ? Je n'en vois aucun.
Pour moi quand je compte le nombre de cartes qu'il faut ajouter à un château à
Et une fois que j'ai ainsi
Alors finalement, où est le problème ? Je n'en vois aucun.
Re: Château de cartes.
Ok je suis d'accord. Je pensais que la formule de un+1 en fonction de u_n et de n n'était que de l'ordre de la conjecture et qu'il fallait encore la redemontrer par reccurence. Pourquoi donc on montre une formule par reccurence et pas l'autre sachant que pour la première on aurait pu dire que de manière combinatoire j'obtiens telle formule.
Re: Château de cartes.
On montre comme on veut, du moment qu'on montre.
Et il me semble plus facile de compter combien de cartes ajouter pour passer de n étages à n+1 étages (pas une conjecture, un vrai calcul justifié de manière argumentée) que de compter directement combien de cartes il faut pour n étages.
Et il me semble plus facile de compter combien de cartes ajouter pour passer de n étages à n+1 étages (pas une conjecture, un vrai calcul justifié de manière argumentée) que de compter directement combien de cartes il faut pour n étages.
Re: Château de cartes.
Si vous obtenez u_n+1 en fonction de u_n et de n, il sera plus difficile de calculer u_24 par exemple. Il faudra calculer tous les u_n pour n inférieur à 24. Sauf si on tombe sur une suite classique.
Re: Château de cartes.
Je crois que tu n'as pas compris mon message précédent.
Je dis qu'il est plus facile d'établir la relation de récurrence entre et
et  que d'établir directement une formule close pour
que d'établir directement une formule close pour  .
.
Et une fois qu'on a la relation de récurrence
 +n =u_n+3n+2) (car on ajoute
(car on ajoute  paires de cartes obliques et
paires de cartes obliques et  cartes horizontales),
cartes horizontales),
on peut établir par récurrence la formule close pour à partir de cette relation de récurrence. Soit on intuite cette formule close à partir du cas de petits
à partir de cette relation de récurrence. Soit on intuite cette formule close à partir du cas de petits  et on la démontre par récurrence, soit on procède méthodiquement : puisque
et on la démontre par récurrence, soit on procède méthodiquement : puisque  est un polynôme de degré 1 en
est un polynôme de degré 1 en  et que
et que 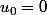 ,
,  est un polynôme de degré 2 en
est un polynôme de degré 2 en  sans terme constant :
sans terme constant : 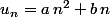 , et on trouve
, et on trouve  et
et  en identifiant
en identifiant ^2+b\,(n+1) - a\,n^2-b\,n) avec
avec  , ce qui donne
, ce qui donne 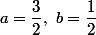 .
.
Je dis qu'il est plus facile d'établir la relation de récurrence entre
Et une fois qu'on a la relation de récurrence
on peut établir par récurrence la formule close pour
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
