Centre de symétrie d'une courbe Cf
42 messages
- Page 1 sur 3 - 1, 2, 3
Centre de symétrie d'une courbe Cf
Bonjour à tous,
J'ai un petit problème à résoudre et j'ai besoin de votre aide
l'énoncé :
soit une fonction définie sur IR - {- 2 }
par f(x) : (x² + x -1) / (x+2)
Question :
1) Montrer que Cf admet un centre de symétrie
2) et en déterminer les coordonnées
Alors voilà ou j'en suis je sais que pour montrer qu'une courbe Cf admet un centre de symétrie il y a 2 solutions
soit :
- en effectuant un changement de repère.
- en montrant que le symétrique de tout point de la courbe C par rapport au point O' appartient encore à C :
c'est à dire :
f(a - x) + f(a + x) = 2b pour tout réel x tel que a + x et a - x appartiennent à l'ensemble de définition de Df
--> Je sais que si x est différent de -2 alors x appartient à Df
donc si a-x et a+x sont différent de -2 ils appartiennet à Df
et ensuite ??
c'est la deuxième méthode que je souhaite utiliser mais comme je n'ai pas les coordonnées de I centre de symétrie comment dois je procéder je bloque totalement.
MERCI
J'ai un petit problème à résoudre et j'ai besoin de votre aide
l'énoncé :
soit une fonction définie sur IR - {- 2 }
par f(x) : (x² + x -1) / (x+2)
Question :
1) Montrer que Cf admet un centre de symétrie
2) et en déterminer les coordonnées
Alors voilà ou j'en suis je sais que pour montrer qu'une courbe Cf admet un centre de symétrie il y a 2 solutions
soit :
- en effectuant un changement de repère.
- en montrant que le symétrique de tout point de la courbe C par rapport au point O' appartient encore à C :
c'est à dire :
f(a - x) + f(a + x) = 2b pour tout réel x tel que a + x et a - x appartiennent à l'ensemble de définition de Df
--> Je sais que si x est différent de -2 alors x appartient à Df
donc si a-x et a+x sont différent de -2 ils appartiennet à Df
et ensuite ??
c'est la deuxième méthode que je souhaite utiliser mais comme je n'ai pas les coordonnées de I centre de symétrie comment dois je procéder je bloque totalement.
MERCI
Bien que ton message est peu clair et légèrement calqué sur homéomath , je crois pouvoir t'aider .
Deja essayons ce qu'est b dans l'équation suivante : f(a-x)+f(a+x)=2b .
Cela ressemble beaucoup une moyenne arithmétique . b est le milieu du segment
[f(a-x),f(a+x)] .
Donc le centre de symétrie de la courbe est le point I(a,b)
Deja essayons ce qu'est b dans l'équation suivante : f(a-x)+f(a+x)=2b .
Cela ressemble beaucoup une moyenne arithmétique . b est le milieu du segment
[f(a-x),f(a+x)] .
Donc le centre de symétrie de la courbe est le point I(a,b)
tu comprends bien que nous avons créé l'intervalle[a-x,a+x] de telle sorte que a en soit le milieu .
Si ta courbe est symétrique par rapport à l'axe x=a , alors il est clair que f(a-x)=f(a+x) et à ce moment il s'agit d'un axe et pas d'un point .
Or dans le cas général les fonctions symétriques le sont par rapport à un point ( tiens c'est un bon exercice de déterminer le rapport du nombre de courbes symétriques par rapport à un axe ou a un point ) donc admet pour centre de symétrie le point I(a;[f(a-x)+f(a+x)]/2)
Si ta courbe est symétrique par rapport à l'axe x=a , alors il est clair que f(a-x)=f(a+x) et à ce moment il s'agit d'un axe et pas d'un point .
Or dans le cas général les fonctions symétriques le sont par rapport à un point ( tiens c'est un bon exercice de déterminer le rapport du nombre de courbes symétriques par rapport à un axe ou a un point ) donc admet pour centre de symétrie le point I(a;[f(a-x)+f(a+x)]/2)
Pour ce problème classique du niveau de 1ère, comme tu dis il y a 2 méthodes. Sauf que tu oublies quelque chose pour la 1ère méthode :
1°) est centre de symétrie de
est centre de symétrie de  ssi
ssi  est la courbe représentative d'une fonction
est la courbe représentative d'une fonction  impaire dans
impaire dans  .
.
2°) centre de symétrie de
centre de symétrie de  ssi :
ssi :
 , on a :
, on a :
 .
.
Etant donné que tu ne connais pas les coordonnées de I, Il te faut 2 équations en a et b afin de déterminer ces coordonnées. Tu en as déjà une avec la . Il te fait trouver une autre équation...
. Il te fait trouver une autre équation...
1°)
 est centre de symétrie de
est centre de symétrie de  ssi
ssi  est la courbe représentative d'une fonction
est la courbe représentative d'une fonction  impaire dans
impaire dans  .
.2°)
 centre de symétrie de
centre de symétrie de  ssi :
ssi : , on a :
, on a : .
.Etant donné que tu ne connais pas les coordonnées de I, Il te faut 2 équations en a et b afin de déterminer ces coordonnées. Tu en as déjà une avec la
 . Il te fait trouver une autre équation...
. Il te fait trouver une autre équation...Pour ce problème classique du niveau de 1ère, comme tu dis il y a 2 méthodes. Sauf que tu oublies quelque chose pour la 1ère méthode :
1°)) est centre de symétrie de
est centre de symétrie de  ssi
ssi  est la courbe représentative d'une fonction
est la courbe représentative d'une fonction  impaire dans
impaire dans ;\,\vec i,\vec j)) .
.
2°)) centre de symétrie de
centre de symétrie de  ssi :
ssi :
 , on a :
, on a :
+f(a-h)=2b\end{matrix}) .
.
Etant donné que tu ne connais pas les coordonnées de I, Il te faut 2 équations en a et b afin de déterminer ces coordonnées. Tu en as déjà une avec la+f(a-h)=2b) . Il te fait trouver une autre équation...
. Il te fait trouver une autre équation...
1°)
2°)
Etant donné que tu ne connais pas les coordonnées de I, Il te faut 2 équations en a et b afin de déterminer ces coordonnées. Tu en as déjà une avec la
Pour ce problème classique du niveau de 1ère, comme tu dis il y a 2 méthodes. Sauf que tu oublies quelque chose pour la 1ère méthode :
1°) est centre de symétrie de
est centre de symétrie de  ssi
ssi  est la courbe représentative d'une fonction
est la courbe représentative d'une fonction  impaire dans
impaire dans  .
.
2°) centre de symétrie de
centre de symétrie de  ssi sur
ssi sur  :
:
 , on a :
, on a :
 .
.
Etant donné que tu ne connais pas les coordonnées de , Il te faut 2 équations en
, Il te faut 2 équations en  et
et  afin de déterminer ces coordonnées. Tu en as déjà une avec la
afin de déterminer ces coordonnées. Tu en as déjà une avec la  . Il te fait trouver une autre équation...
. Il te fait trouver une autre équation...
1°)
 est centre de symétrie de
est centre de symétrie de  ssi
ssi  est la courbe représentative d'une fonction
est la courbe représentative d'une fonction  impaire dans
impaire dans  .
.2°)
 centre de symétrie de
centre de symétrie de  ssi sur
ssi sur  :
: , on a :
, on a : .
.Etant donné que tu ne connais pas les coordonnées de
 , Il te faut 2 équations en
, Il te faut 2 équations en  et
et  afin de déterminer ces coordonnées. Tu en as déjà une avec la
afin de déterminer ces coordonnées. Tu en as déjà une avec la  . Il te fait trouver une autre équation...
. Il te fait trouver une autre équation...Pour ce problème classique du niveau de 1ère, comme tu dis il y a 2 méthodes. Sauf que tu oublies quelque chose pour la 1ère méthode :
1°)) est centre de symétrie de
est centre de symétrie de  ssi
ssi  est la courbe représentative d'une fonction
est la courbe représentative d'une fonction  impaire dans
impaire dans ;\,\vec i,\vec j)) .
.
2°)) centre de symétrie de
centre de symétrie de  ssi sur
ssi sur  :
:
 , on a :
, on a :
+f(a-h)=2b\end{matrix}) .
.
Etant donné que tu ne connais pas les coordonnées de , Il te faut 2 équations en
, Il te faut 2 équations en  et
et  afin de déterminer ces coordonnées. Tu en as déjà une avec la
afin de déterminer ces coordonnées. Tu en as déjà une avec la +f(a-h)=2b) . Il te fait trouver une autre équation...
. Il te fait trouver une autre équation...
1°)
2°)
Etant donné que tu ne connais pas les coordonnées de
C'est une très bonne méthode Phryte.:++:
Définition des asymptotes horizontale (y=k) et verticales (x=m) :
Si alors
alors  est asympote horizontale de
est asympote horizontale de  .
.
Si alors
alors  est asympote horizontale de
est asympote horizontale de  .
.
Définition des asymptotes horizontale (y=k) et verticales (x=m) :
Si
 alors
alors  est asympote horizontale de
est asympote horizontale de  .
.Si
 alors
alors  est asympote horizontale de
est asympote horizontale de  .
.saske a écrit:Merci
-deux questions qu'est ce qu'une asymptote (je sens que je fais me faire linché) ?
- et tu trouve -2 car je supprose que c'est par rapport à IR - { -2} ?
J'ai vraiment du mal avec c'est cours par correspondance Désolé
C'est une très bonne méthode Phryte.:++:
Définition des asymptotes horizontale ( ) et verticales (
) et verticales (  ) :
) :
Si alors
alors  est asymptote horizontale de
est asymptote horizontale de  .
.
Si alors
alors  est asymptote horizontale de
est asymptote horizontale de  .
.
Définition des asymptotes horizontale (
 ) et verticales (
) et verticales (  ) :
) :Si
 alors
alors  est asymptote horizontale de
est asymptote horizontale de  .
.Si
 alors
alors  est asymptote horizontale de
est asymptote horizontale de  .
.saske a écrit:Merci
-deux questions qu'est ce qu'une asymptote (je sens que je fais me faire linché) ?
- et tu trouve -2 car je supprose que c'est par rapport à IR - { -2} ?
J'ai vraiment du mal avec c'est cours par correspondance Désolé
C'est une très bonne méthode Phryte.:++:
Définition des asymptotes horizontale (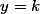 ) et verticales (
) et verticales (  ) :
) :
Si=k) alors
alors 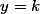 est asymptote horizontale de
est asymptote horizontale de  .
.
Si=\pm\infty) alors
alors  est asymptote horizontale de
est asymptote horizontale de  .
.
Définition des asymptotes horizontale (
Si
Si
saske a écrit:Merci
-deux questions qu'est ce qu'une asymptote (je sens que je fais me faire linché) ?
- et tu trouve -2 car je supprose que c'est par rapport à IR - { -2} ?
J'ai vraiment du mal avec c'est cours par correspondance Désolé
42 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
