Centre de symétrie d'une courbe Cf

[saske]

si x = -2

(-2) - 1 + 1 / -2 + 2
y = -2 / 0

[phryte]

Si x =-2 alors x-1 vaut :

[saske]

oui j'ai été trop vite
-3 + 1 / -2 + 2
y = -2 / 0

[phryte]

Non -2 -1 = -3

[saske]

oui je suis d'accord -2 -1 = -3 donc x -1 +1 / x +2
c'est bien égale à -2 -1 +1 /-2+2
-3+1/0
-2/0
non??

j'ai repris l'équation donnée au départ

[Fanatic]

J'ai oublié de définir les asymptotes obliques.
La droite d'équation est asymptote oblique de ssi :
.
Or on t'a écris que .
Donc .
Ainsi admet une asymptote verticale d'équation et une asymptote oblique d'équation .
Il suffit d'injecter x=-2 dans y=x-1 et tu trouves l'ordonnée du centre de symétrie de . a pour coordonnées .
Je te laisse terminer.

[Fanatic]

J'ai oublié de définir les asymptotes obliques.
La droite d'équation est asymptote oblique de ssi :
.
Or on t'a écris que .
Donc .
Ainsi admet une asymptote verticale d'équation 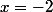et une asymptote oblique d'équation .
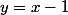Il suffit d'injecter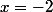 dans 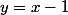et tu trouves l'ordonnée du centre de symétrie de . a pour coordonnées .
Je te laisse terminer.

[Fanatic]

Phryte est beaucoup plus rapide que moi...
Désolé pour les messages croisés ou dupliqués...
Merci Phryte :++:

[saske]

Ah ok je comprends mieux oui donc dans ce cas là y = -3
et x =-2 donc I(-2 ; -3)
est le centre de symétrie de la courbe représentée par f(x)

Merci.

Edit : tu n'as pas à être désolé au contraire merci de ton aide mais je ne comprenais plus pourquoi phryte insisté sur y = -3 lol

[Fanatic]

OUI c'est bien, tu peux remercier Phryte.
Et note le résumé de cours de mes posts, ça te servira pour étudier une fonction...
Finalement, tu peux rajouter cette 3ème méthode qui marche uniquement pour les hyperboles :
avec les éventuelles asymptotes horizontale, verticale, oblique de .

Ah ok je comprends mieux oui donc dans ce cas là y = -3
et x =-2 donc I(-2 ; -3)
est le centre de symétrie de la courbe représentée par f(x)

Merci.

[saske]

merci phryte lol

[saske]

donc si I (-2 , -3) l'équation [f(2a-x) + f(x)]/2 = b doit se vérifier en remplaçant a par -2 et x par f(x) = [x² + x-1] / x+2

ce qui nous donne 2(-2) - [[x² + x-1] / x+2] + [x² + x-1] / x+2 = 2b
mais en calculant je ne trouve pas le bon résultat je ne trouve pas 2b donc -6

[Weensie]

quel cours splendide fanatic et phryte , pardonnez moi pour mon absence

[saske]

personne pour la solution ?

[Black Jack]

saske, tu confonds f(2a-x) avec 2a - f(x). :hein: :hein:


f(x) = (x² + x -1) / (x+2)

avec a = -2

f(2a-x) = f(-4-x) = ((-4-x)² -4 - x -1) / (-4-x+2) = ...

Continue.

:zen:

[saske]

Donc si je résolve cette équation le résultat me donnera x ?
et avec x et a je pourrai prouver b ??

Oula désolé mais je galère comme pas possible.

[Fanatic]

Mais pourquoi tu galères, fait ce qu'on t'a dit dernièrement si tu veux absolument utiliser cette méthode, sinon, tu as juste à déterminer le point d'intersection des 2 asymptotes 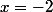et 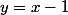tout simplement. Tu as 3 méthodes que je t'ai donné avec Phryte mais celle des asymptotes est la plus rapide à condition que tu saches calculer des limites...
@+

Donc si je résolve cette équation le résultat me donnera x ?
et avec x et a je pourrai prouver b ??

Oula désolé mais je galère comme pas possible.

[saske]

c'est par rapport à mes cours qui ne donne pas du tout cette méthode et sur un exemple pour prouver que la courbe cf a un centre de symétrie ils définissent deux conditions
soit :

si x appartient à Df alors 2a - x appartient à Df
et
pour tout x appartenant à Df il faut que
[(f(2a-x) - f(x)) / 2] = b

donc le but c'est de montrer en calculant cette équation que le résultat trouvé se trouve etre b donc -3
ce qui nous permettrai de prouver que c'est deux conditions sont respectées et donc que Cf à bien un centre de symétrie
après on me demande de calculer les coordonées de ce centre de symétrie ca vous me l'avez expliqué même si j'ai pas tout cerné mais ca donne :
soit I centre de symétrie (-2 ; -3)

je voulais seulement utiliser la même méthode que celle du cours pour pas m'en éloigner.

[saske]

et je pense que mes lacunes sont plus lointaines donc il faudrait que je reprenne l'étude d'une fonction au complette sinon je sens que pour les autre cours je risque de nager

[Fanatic]

En fait tu ne comprends pas bien la propriété que tu utilises on a, et :
Pour tout on a :


Mettre à la place de évite les confusions...
Donc cette expression est variable donc en particulier pour par exemple. Il vient :

On calcule bien des images de nombres appartenant à l'ensemble de définition de et on obtient bien .
CQFD.