Centre et axe d'une similitude indirecte
12 messages
- Page 1 sur 1
centre et axe d'une similitude indirecte
Soient 4 points différentes A, B, A" et B", comment construire l'axe et le centre de la similitude indirecte qui transforme A en A" et B en B"
Re: centre et axe d'une similitude indirecte
peut être en se servant de la "conservation" des centres et des droites
Re: centre et axe d'une similitude indirecte
salut
si s est la similitude alors considérer les vecteurs
} \ et \ \vec {Bs(B)})
et
s(B)}) ...
...
si s est la similitude alors considérer les vecteurs
et
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: centre et axe d'une similitude indirecte
Bonjour,
On a le choix (sans être exhaustif):
On cherche le centre et l' axe
et l' axe ) de la similitude indirecte
de la similitude indirecte  qui envoie
qui envoie  sur
sur 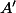 et
et  sur
sur 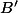 donnés tels que
donnés tels que 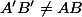
1) On sait (ou pas ?) que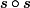 est l' homothétie de centre
est l' homothétie de centre  et de rapport
et de rapport 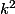 où
où 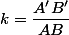 est le rapport de la similitude.
est le rapport de la similitude.
On construit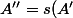) et
et 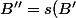)
L' intersection des droites) et
et ) est le centre
est le centre  cherché.
cherché.
L' axe) est la bissectrice de
est la bissectrice de )
2) On a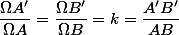
 est une des deux intersections de deux cercles d' Apollonius. Il faut choisir: l' autre intersection est le centre de la similitude directe envoyant
est une des deux intersections de deux cercles d' Apollonius. Il faut choisir: l' autre intersection est le centre de la similitude directe envoyant  sur
sur 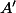 et
et  sur
sur 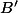
3) Une autre construction; je te laisse le soin de découvrir pourquoi elle "marche".
La direction de l' axe est celle de la bissectrice de)
On trace la droite) passant par
passant par 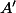 et parallèle à cet axe.
et parallèle à cet axe.
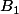 est le symétrique de
est le symétrique de  par rapport à
par rapport à )
) et
et ) se coupent en
se coupent en  (voir pourquoi elles ne sont pas parallèles)
(voir pourquoi elles ne sont pas parallèles)
 est le pied de la perpendiculaire issue de
est le pied de la perpendiculaire issue de  sur
sur )
 est le milieu de
est le milieu de 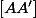
La parallèle à) passant par
passant par  recoupe
recoupe ) au point
au point 
On achève la construction en menant la parallèle) à
à ) passant par
passant par 

On a le choix (sans être exhaustif):
On cherche le centre
1) On sait (ou pas ?) que
On construit
L' intersection des droites
L' axe
2) On a
3) Une autre construction; je te laisse le soin de découvrir pourquoi elle "marche".
La direction de l' axe est celle de la bissectrice de
On trace la droite
La parallèle à
On achève la construction en menant la parallèle
- Fichiers joints
-
- MF1.png (18.6 Kio) Vu 5339 fois
Modifié en dernier par cailloux1 le 14 Aoû 2017, 10:44, modifié 2 fois.
Re: centre et axe d'une similitude indirecte
Arf! des problèmes de cadrage de figure 
Je ne sais pas trop comment m' y prendre; les pixels étaient bons...
Bon, j' ai édité...
Je ne sais pas trop comment m' y prendre; les pixels étaient bons...
Bon, j' ai édité...
Re: centre et axe d'une similitude indirecte
j'ai testé la 3 ième méthode, elle est juste mais très lente (manque les explications)
Re: centre et axe d'une similitude indirecte
babahamda a écrit:j'ai testé la 3 ième méthode, (manque les explications)
Il faut bien que tu fasses quelque chose! Je t' avais indiqué:
je te laisse le soin de découvrir pourquoi elle "marche".
Eh oui, il faut chercher, réfléchir, faire des mathématiques en somme
Re: centre et axe d'une similitude indirecte
Salut,
j'ai résolu ce problème depuis presque un an, mais toujours je cherche ailleurs pour voir d'autres méthodes plus simples,
je propose la méthode la plus simple mais n'est pas encore démontré
- soit J l'intersection de deux droites (AB') et (A'B)
- Soit E milieu de [AA'] et F milieu de [BB']
- le centre de la similitude indirecte appartient à la droite parallèle à (EF) et passant par J
j'ai résolu ce problème depuis presque un an, mais toujours je cherche ailleurs pour voir d'autres méthodes plus simples,
je propose la méthode la plus simple mais n'est pas encore démontré
- soit J l'intersection de deux droites (AB') et (A'B)
- Soit E milieu de [AA'] et F milieu de [BB']
- le centre de la similitude indirecte appartient à la droite parallèle à (EF) et passant par J
Re: centre et axe d'une similitude indirecte
je propose la méthode la plus simple
- le centre de la similitude indirecte appartient à la droite parallèle à (EF) et passant par J
Peut-être, je n' ai pas vérifié mais en tout état de cause, ta "méthode" ne permet pas de déterminer le centre cherché. Au mieux, tu conjectures que ce centre appartient à une certaine droite. On est encore loin du compte...

Re: centre et axe d'une similitude indirecte
Le centre  appartient bien à ta droite (en bleu sur la figure). Mais pour le déterminer, il faut un second lieu;
appartient bien à ta droite (en bleu sur la figure). Mais pour le déterminer, il faut un second lieu;
Par exemple l' axe de la similitude: les points et
et  qui divisent les segments
qui divisent les segments 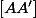 et
et 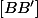 dans le rapport
dans le rapport 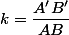 (le rapport de la similitude) appartiennent à cet axe.
(le rapport de la similitude) appartiennent à cet axe.
D' où une 4ème construction:

Par exemple l' axe de la similitude: les points
D' où une 4ème construction:
Re: centre et axe d'une similitude indirecte
Thalès par exemple:
On reporte les longueurs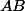 et
et 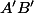 sur deux parallèles en
sur deux parallèles en 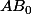 et
et 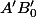
) recoupe le segment
recoupe le segment 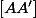 en
en 

[Edit] tout va mieux à présent
On reporte les longueurs
[Edit] tout va mieux à présent
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
