Similitude indirecte , forum complexe

[mascor]

Salut
Voici une partie d exercice , jai pas aarive a resoudre 1) b et 2) b
http://img15.hostingpics.net/pics/901211201406012154071.jpg

[paquito]

1)a) f est sous la forme z'=a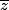+b, donc c'est une similitude indirecte.

Ensuite, il faut résoudre z=-2i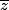+1+2i; on passe à l'égalité conjuguée:

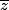=2iz+1-2i; on remplace 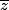par 2iz+1-2i, on fait le
calcul et on obtient z=1; I est bien le centre de f.

b) l'axe est caractérisé par z'-1=k(z-1), où k>0 est le rapport de f; utilisons l'énoncé et posons

z=x+i(1-x); on obtient z'-1=-2i(x-i(1-x))+2i=2(x+i(1-x)-1)=2(z-1) (Calculs à refaire);

donc l'axe de f est bien la droite d'équation y=1-x et de plus le rapport de f est 2.

2)a) f rond f est une similitude directe et même ici une homothétie de rapport k=4 et de centre I;
f(f(z))=z''=-2i(2iz+1-2i)+1+2i=4z-3; on a bien z"-1=4(z-1).

b) s'obtient par récurrence et par f()

c) question de cours.

[mascor]

1)a) f est sous la forme z'=a+b, donc c'est une similitude indirecte.

Ensuite, il faut résoudre z=-2i+1+2i; on passe à l'égalité conjuguée:

=2iz+1-2i; on remplace par 2iz+1-2i, on fait le
calcul et on obtient z=1; I est bien le centre de f.

b) l'axe est caractérisé par z'-1=k(z-1), où k>0 est le rapport de f; utilisons l'énoncé et posons

z=x+i(1-x); on obtient z'-1=-2i(x-i(1-x))+2i=2(x+i(1-x)-1)=2(z-1) (Calculs à refaire);

donc l'axe de f est bien la droite d'équation y=1-x et de plus le rapport de f est 2.

2)a) f rond f est une similitude directe et même ici une homothétie de rapport k=4 et de centre I;
f(f(z))=z''=-2i(2iz+1-2i)+1+2i=4z-3; on a bien z"-1=4(z-1).

b) s'obtient par récurrence et par f()

c) question de cours.

Merci b1 pour votre reoonse paquito