Cas d'égalité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
qelmcpc
- Membre Naturel
- Messages: 72
- Enregistré le: 07 Avr 2014, 18:23
-
 par qelmcpc » 25 Juil 2014, 14:09
par qelmcpc » 25 Juil 2014, 14:09
Bonjour à tous,
Dans un exercice, je dois trouver la condition nécessaire et suffisante telle que l'inégalité de Cauchy - Schwarz devienne une égalité.
(L'inégalité au cas où:
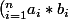^2 \leq \bigsum_{i=1}^{n} (a_i)^2 * \bigsum_{i=1}^{n} (b_i)^2)
Mais je ne vois pas trop comment faire...
Voilà, merci beaucoup!

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 25 Juil 2014, 16:46
par WillyCagnes » 25 Juil 2014, 16:46
-
qelmcpc
- Membre Naturel
- Messages: 72
- Enregistré le: 07 Avr 2014, 18:23
-
 par qelmcpc » 25 Juil 2014, 16:54
par qelmcpc » 25 Juil 2014, 16:54
Merci pour le lien. Par contre, j'ai pas trop compris le : "les vecteur x et y sont liés" :/
je ne connais que l'inégalité "numérique"

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Juil 2014, 16:56
par zygomatique » 25 Juil 2014, 16:56
salut
que penses-tu de b = ka ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
qelmcpc
- Membre Naturel
- Messages: 72
- Enregistré le: 07 Avr 2014, 18:23
-
 par qelmcpc » 25 Juil 2014, 17:07
par qelmcpc » 25 Juil 2014, 17:07
Effectivement, ça marche!
Auriez-vous une démonstration pour le prouver?
-
qelmcpc
- Membre Naturel
- Messages: 72
- Enregistré le: 07 Avr 2014, 18:23
-
 par qelmcpc » 26 Juil 2014, 08:33
par qelmcpc » 26 Juil 2014, 08:33
J'ai toruvé sur Internet cet identité:
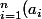^2 * \bigsum_{i=0}^{n} (b_i)^2 = (\bigsum_{i=0}^{n} a_i*b_i)^2 + \bigsum_{0\lt i \lt j \leq n}^{} (a_i*b_j - a_j * b_i )^2)
Ca résoud normalement le problème :ptdr:
-
qelmcpc
- Membre Naturel
- Messages: 72
- Enregistré le: 07 Avr 2014, 18:23
-
 par qelmcpc » 26 Juil 2014, 12:23
par qelmcpc » 26 Juil 2014, 12:23
Merci beaucoup!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités