Cas de probabilité simple

[Dante0]

Bonjour,

J'aimerais comprendre une erreur qui m'arrive souvent lorsque je fais face à des probabilités.
Exemple :

On étudie un paquet de cartes un peu particulières. Chaque carte comporte un (et un seul) symbole.
Les symboles diffèrent par leur forme et leur couleur. Il y a trois formes (le carré, le disque et le triangle)
et deux couleurs (noir et rouge). Il existe, par exemple, des cartes comportant un carré rouge, d’autres
un disque noir, etc. Plus précisément le paquet étudié contient le nombre de cartes indiqué dans le
tableau ci-dessous :

Couleurs/forme carré disque triangle
noir 2 4 1
rouge 3 1 2

On tire 3 cartes et je cherche la probabilité que les 3 cartes soient des cartes ayant un disque noir.
Ce que j'aurais fait instinctivement : je me dis qu'il y'a 13 cartes au total et donc la probabilité pour tirer une carte disque noir est de 4/13.
Comme on est dans un cas sans remise, la probabilité de tirer 3 cartes disque noir suivies est de 4/13*3/13*2/13 non ?
Or ce n'est pas le cas donc j'aimerais savoir ce que je ne prends pas en compte et à quoi correspond mon calcul...

Merci ! =)

[Iroh]

1 On tire 3 cartes, une par une, sans remise
;););););););););););););););););););););););););););););););)

1.1 Les cartes sont numérotées.
;);););););););););););););););););););););)

Elles ont donc toutes la même chance d'être piochées. On note une
carte par: . Exemple: La carte carré noir n°1
est notée: NC1. Quels sont les tirages favorables ?

1. 1e carte: ND1, 2e: ND2, 3e: ND3 (on note: [ND1,ND2,ND3])
2. [ND2,ND1,ND3]
3. [ND4,ND2,ND1]
4. etc.

• La probabilité d'avoir le tirage 1.: proba d'avoir la carte ND1 =
, puis d'avoir la carte ND1 = 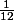(car
plus que 12 cartes), puis d'avoir la carte ND3 = .
La proba d'avoir le tirage [ND1,ND2,ND3] =
• La probabilité d'avoir le tirage 2:
• etc.

Pour tirer 3 disques noir consécutivement, on peut donc réaliser le
tirage [ND1,ND2,ND3] OU [ND2,ND1,ND3] OU …. On fait la somme entre
ces probabilités.

Reste à connaitre le nombre de tirages favorable possibles: les cartes
sont distinguables: l'ordre compte. Chaque tirage consiste en un
arrangement de 3 disques noirs par mis 4:

La probabilité vaut donc:


1.2 Les cartes ne sont pas numérotées.
;););););););););););););););););););););););););););)

Elles n'ont pas toutes la même chance d'être piochées. On note une
carte par: . Exemple: une carte carré noir est notée:
NC. Seule possibilité de tirage favorable: [ND,ND,ND].

Premier tirage: proba d'avoir un disque noir = .
Deuxième tirage: proba d'avoir un disque noir: (car il
n'y a plus que 4 disques noir et que 12 cartes au total). Troisième
tirage: proba d'avoir un disque noir vaut .

La probabilité vaut donc au final: .


2 On tire 3 cartes simultanément.
;););););););););););););););););););););););)

On numérote les cartes. Toutes les cartes ont donc la même chance
d'être piochée: La proba vaut le rapport entre le nombre de cas
favorables et le nombre de cas possibles.


2.1 Quand on a pioché 3 cartes, on tient compte de l'ordre.
;);););););););););););););););););););););););););););););););););););););););););)

Cas favorables: {[NC1,NC2,NC3], [NC2, NC1, NC4], …}. Nombre de cas
favorables: arrangement de 3 cartes (disque noir) parmi 4:

Cas possibles: arrangement de 3 cartes (n'importe lesquelles) parmi
toutes:

La proba vaut: .


2.2 Quand on a pioché 3 cartes, on ne tient pas compte de l'ordre.
;););););););););););););););););););););););););););););););););););););););););););););););)

Cas favorables: {[NC1,NC2,NC3], [NC1,NC2,NC4], [NC1,NC3,NC4],
[NC2,NC3,NC4]}. Le nombre de cas favorables: combinaison de 3 cartes
(disque noir) parmi 4:

Cas possibles: combinaison de 3 cartes (n'importe lesquelles) parmi
toutes:

La proba vaut:

[Dante0]

Merci pour ta réponse bien développée ! :we:
Quand tu dis on ne tient pas compte de l'ordre avec les combinaisons on admet forcément que le tirage se fait avec remise n'est-ce pas ?

Si maintenant on imagine qu'il y'a non pas 4 cartes au disque noir mais seulement 3. Quelle est la probabilité que les 3 cartes tirées soient des cartes au disque noir ?

3/13 * 2/12 * 1/11 ?

[Iroh]

Non, le développement explique plusieurs expériences qui ont la même chance de
se produire: dans ton jeu de carte, probabilité d'avoir 3 disques noirs.

Tu considères deux types d'expérience:
1. Tu pioches une carte après l'autre (sans remise)
2. Tu pioches 3 cartes d'un coup (donc pas possible d'avoir plusieurs fois la même carte)


Pour le 1.:
1.1 soit tu numérotes les cartes, alors tu distingues le fait de piocher la carte
disque noir n°1, puis la disque noir n°2 puis la n°3, avec le fait de piocher
la carte disque noir n°3 en premier par exemple.
1.2 soit tu ne numérotes pas les cartes, et là tu ne peux pas savoir quelle carte
disque noir tu as avant l'autre comme elle ne sont pas numérotée.

Pour le 2. tu numérotes d'office toute les cartes pour les distinguer (sans les
ça il est plus dur de calculer les combinaisons)
2.1 soit quand tu les as en mains tu décides de tenir compte de l'ordre: celle à
gauche de ta main est la première, celle à droite la dernière, celle au milieu
la deuxième.
2.2 soit quand tu les as en mains, tu ne regardes pas les numéros et considère que
le fait d'avoir la carte disque noir n°1 à gauche ou à droite de ta main n'a pas
d'importance.


Si tu as 3 cartes disques noirs, tu peux appliquer le même raisonnement pour les
4 points, tu dois avoir la même probabilité.

[Dante0]

Non, le développement explique plusieurs expériences qui ont la même chance de
se produire: dans ton jeu de carte, probabilité d'avoir 3 disques noirs.

Tu considères deux types d'expérience:
1. Tu pioches une carte après l'autre (sans remise)
2. Tu pioches 3 cartes d'un coup (donc pas possible d'avoir plusieurs fois la même carte)


Pour le 1.:
1.1 soit tu numérotes les cartes, alors tu distingues le fait de piocher la carte
disque noir n°1, puis la disque noir n°2 puis la n°3, avec le fait de piocher
la carte disque noir n°3 en premier par exemple.
1.2 soit tu ne numérotes pas les cartes, et là tu ne peux pas savoir quelle carte
disque noir tu as avant l'autre comme elle ne sont pas numérotée.

Pour le 2. tu numérotes d'office toute les cartes pour les distinguer (sans les
ça il est plus dur de calculer les combinaisons)
2.1 soit quand tu les as en mains tu décides de tenir compte de l'ordre: celle à
gauche de ta main est la première, celle à droite la dernière, celle au milieu
la deuxième.
2.2 soit quand tu les as en mains, tu ne regardes pas les numéros et considère que
le fait d'avoir la carte disque noir n°1 à gauche ou à droite de ta main n'a pas
d'importance.


Si tu as 3 cartes disques noirs, tu peux appliquer le même raisonnement pour les
4 points, tu dois avoir la même probabilité.

Je ne vois pas de différence entre les 2 phrases en gras, dans tous les cas c'est impossible de tirer 2 fois la même carte si ?
Je comprends pas ce que tu essayes d'expliquer par la suite..

[Dante0]

Petit up j'arrive toujours pas à comprendre :(

[Iroh]

Oui c'est juste dans les deux cas on ne peut pas piocher deux fois la même carte. Tu ne comprends pas quoi sinon ?

[Dante0]

La réponse que tu m'as apportée à propos de cette question :

Si maintenant on imagine qu'il y'a non pas 4 cartes au disque noir mais seulement 3. Quelle est la probabilité que les 3 cartes tirées soient des cartes au disque noir ?

3/13 * 2/12 * 1/11 ?

[Iroh]

Quelle est l'expérience exactement: tu tires 3 d'un coup, ou une après l'autre sans remise ?

[Dante0]

Quelle est l'expérience exactement: tu tires 3 d'un coup, ou une après l'autre sans remise ?

Mais justement je vois pas de différence entre tirer 3 d'un coup ou une après l'autre sans remise, ca revient au même non ? Dans les 2 cas, lorsqu'on tire une carte, ca influe sur la probabilité de tirer la carte suivante, l'ordre compte.

[Iroh]

L'expérience est différente, les calculs sont différents, la probabilité obtenue est la même.

De plus, que tu décides de tenir compte de l'ordre ou pas, la probabilité obtenue est encore la même (seuls changent les calculs)

Points 1.1 et 2.1: tiennent comptent de l'ordre
Points 1.2 et 2.2: ne tiennent pas compte de l'ordre

[Dante0]

A quel moment on sait si on s'intéresse à l'ordre ou non ? C'est bien si on est dans le cas d'un tirage avec remise (l'ordre ne compte pas) ou sans remise (l'ordre compte) exact ?

[Iroh]

Ici on ne considère que les 2 cas suivants:
1. Tirage de plusieurs cartes consécutivement sans remise (on tire une carte après l'autre)
2. Tirage de plusieurs cartes simultanément (on ne peut jamais piocher deux fois la même carte dans ce cas, donc jamais de «remise»)


Dans notre cas l'ordre était un choix. Considérons le premier cas: c'est-à-dire le tirage de plusieurs cartes l'une après l'autre sans remise. Tu cherches la probabilité de tirer 3 disques noirs.

Supposons qu'on ne sache pas distinguer les 3 disques noirs (les cartes sont identiques). Tu calcules la probabilité de piocher 3 disques noirs.

Maintenant, supposons que tu prennes un bic et que tu numérotes les disques noirs; tu peux dès lors les distinguer: tu auras une carte disque noir portant le numéro 1 par exemple, l'autre le numéro 2 puis le 3, etc. Tu calcules ensuite à nouveau la probabilité de piocher 3 disques noirs. Penses-tu que cette probabilité seras différente ? (Juste parce que tu as écrit des numéros sur des cartes ?)

[Dante0]

Okay merci
Sinon comment calculer la probabilité de tirer exactement une carte carré rouge ?

[Black Jack]

Il ne faut pas faire des calculs pour distinguer des cas qui manifestement ne peuvent donner que des résultats identiques.

Si dans 13 cartes, il y a exactement 3 disques noirs.

Et qu'on cherche la proba de tirer sans remises en 3 cartes les 3 disques noirs, il est évident que le résultat final sera le même que :

- les cartes soient tirées simultanément.
- les cartes soient retirées une par une (sans remise évidemment) et ceci que les cartes soient ou non marquées par des numéros distinctifs.

La proba esr calculée instantanément par : 3/13 * 2/12 * 1/11 et tout le reste ne peut que noyer le poisson ou servir à s'égarer.
*****

Maintenant si on est dans un jeu de 13 cartes avec 4 disques noirs :

Si on veut tirer 3 disques noirs en 3 cartes, il est évident que :

La proba est la même que les cartes soient retirées simultanément ou bien une par une sans remise.

Et dans le cas où on aurait en plus les cartes marquées (par un numéro), l'énoncé devrait alors préciser si le tirage impose aussi les numéros de cartes à tirer ...

Si c'est non, alors le problème est inchangé, si c'est oui, alors le problème revient à chercher la proba de tirer, sans remise, 3 cartes spécifiques dans un tas de 13 cartes. (3/13 * 2/12 * 1/11)

Si de plus, l'énoncé impose l'ordre de tirage des cartes par le numéro (cas de tirage 1 par 1), alors la proba est immédiatement de 1/13 * 1/12 * 1/11 si c'est sans remise ... et (1/13)² si c'est avec remise.
*****

Rien ne sert de faire du calcul pour la "beauté du geste" quand on peut le court-circuiter par un raisonnement simple.

Mais ce n'est que mon avis de profane.

:zen:

[Dante0]

Si de plus, l'énoncé impose l'ordre de tirage des cartes par le numéro (cas de tirage 1 par 1), alors la proba est immédiatement de 1/13 * 1/12 * 1/11 si c'est sans remise ... et (1/13)² si c'est avec remise.
*****


:zen:

Qu'est-ce que tu entends par "par le numéro" ? C'est dans le cas ou les 13 cartes sont identiques ?

[Black Jack]

Qu'est-ce que tu entends par "par le numéro" ? C'est dans le cas ou les 13 cartes sont identiques ?

C'est dans le cas où en plus de la distinction par couleur et forme, chacune des cartes serait en plus numétotées.

On pourrait par exemple avoir (ce n'est pas le cas de l'énoncé initial) parmi les 13 cartes :
- une carte disque noir avec un numero 1
- une carte disque noir avec un numero 2
- une carte disque noir avec un numero 3
- une carte disque noir avec un numero 4

... et on demanderait de tirer dans les 13 cartes, dans l'ordre les 3 disques noirs portant le n° 2 et puis la n° 1 et puis la numéro 4.



:zen:

[Dante0]

Compris merci
Je reviens sur cette question alors :

Sinon comment calculer la probabilité de tirer exactement une carte carré rouge ?

[Black Jack]

Compris merci
Je reviens sur cette question alors :

Il y a 3 carrés rouges sur les 13 cartes.

Sans remise :

a) proba de tirer dans l'ordre 1 carré rouge et puis 2 autres : 3/13 * 10/12 * 9/11
b) proba de tirer dans l'ordre 1 autre , 1 carré rouge et puis 1 autre : 10/13 * 3/12 * 9/11
c) proba de tirer dans l'ordre 2 autres et puis un carré rouge : 10/13 * 9/12 * 3/11

Et donc la proba d'avoir exactement 1 carré rouge est : 3 * 3/13 * 10/12 * 9/11 = 135/286

On a évidemment le même résultat final si on tire les 3 cartes simultanément.

:zen:

[Dante0]

Il y a 3 carrés rouges sur les 13 cartes.

Sans remise :

a) proba de tirer dans l'ordre 1 carré rouge et puis 2 autres : 3/13 * 10/12 * 9/11
b) proba de tirer dans l'ordre 1 autre , 1 carré rouge et puis 1 autre : 10/13 * 3/12 * 9/11
c) proba de tirer dans l'ordre 2 autres et puis un carré rouge : 10/13 * 9/12 * 3/11

Et donc la proba d'avoir exactement 1 carré rouge est : 3 * 3/13 * 10/12 * 9/11 = 135/286

On a évidemment le même résultat final si on tire les 3 cartes simultanément.

:zen:

Pourquoi tu multiplies 3/13 * 10/12 * 9/11 par 3 ? Pourquoi avoir choisi la première proposition ?