Je ne suis pas très fort en maths, surtout sur les fonctions, alors j'aimerais bien de l'aide. Voici l'énoncé :
On dispose d'un carré de métal de 25 cm de côté. Pour fabriquer une boîte sans couvercle, on enlève à chaque coin un carré de côté x et on relève les bords par pliage.
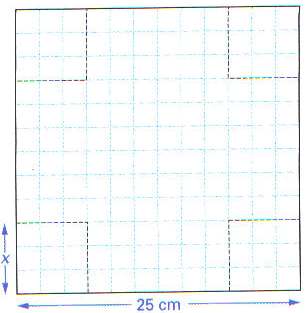
Partie 1:
A)
1) Calculer le volume de la boîte obtenue si x=2.
2) Exprimer le volume V en fonction de x.
On note V= f(x)
3) x peut il prendre toutes les valeurs? Presicez l'ensemble de definition de f ?
4) A quelle condition x est-il une volume nul ?
B) On vient de definir une fonction qui, à tous nombre x de l'intervalle [0;12.5] associe le volume V=f(x) de la boîte.
1) A l'aide de la calculatrice, recopier et compléter le tableau de valeur suivant (image n°1)
2) Sur une feuille de papier millimétré, placer dans un repère convenablement choisi les points dont les coordonnées (x ; f(x)) figurent dans le tableau ci dessus (image n°1) et tracer la courbe ainsi obtenue.
3) Résoudre graphiquement les équations : f(x)=500 et f(x)=1000
Partie 2
L'examen de cette courbe laisse entrevoir que le volume est maximal pour une valeur x0 de x
1) En utilisant la courbe precedente indiquer entre quelles valeurs entieres est compris la valeur x0
2) Donner un tableau de valeur de la fonction f sur [4;4,5] avec un pas de 0,1. Que constate-t-on?
3) Dresser le tableau de variation de la fonction f.
image 1:

