Calculer phi a cube

par **totor60** » 31 Déc 2015, 12:21

Bonjour à tous,

J'ai besoin de votre aide car, dans un dm que j'ai a rendre pour la rentrée, on me demande de calculer phi au cube puis phi4. J'ai déja essayé de faire les calculs mais la je bloque et je ne trouve pas de vraie solutions.

En espérant que quelqu'un pourra m'aider !

Merci d'avance

par **laetidom** » 31 Déc 2015, 12:22

totor60 a écrit:Bonjour à tous,

J'ai besoin de votre aide car, dans un dm que j'ai a rendre pour la rentrée, on me demande de calculer phi au cube puis phi4. J'ai déja essayé de faire les calculs mais la je bloque et je ne trouve pas de vraie solutions.

En espérant que quelqu'un pourra m'aider !

Merci d'avance

Bonjour, ...et

= ....?

on te demande

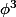
et

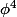
? C'est ça ?....

par **Lostounet** » 31 Déc 2015, 12:26

Salut, est-ce le nombre d'or?

Si oui, on peut remarquer que:
Phi^2=phi + 1
Donc phi^3=phi^2+phi
=2phi + 1

par **totor60** » 31 Déc 2015, 12:26

Bonjour,
pour phi = (1+racine5)/2
et non c'est phi au cube et non au carré et phi exposant 4

par **totor60** » 31 Déc 2015, 12:27

Lostounet a écrit:Salut, est-ce le nombre d'or?

Si oui, on peut remarquer que:
Phi^2=phi + 1
Donc phi^3=phi^2+phi
=2phi + 1

Oui, c'est le nombre d'or

par **totor60** » 31 Déc 2015, 12:31

Ok pour phi au cube et donc pour phi^4, je fait phi^3+phi c'est cela ?

par **laetidom** » 31 Déc 2015, 12:33

Lostounet a écrit:Salut, est-ce le nombre d'or?

Si oui, on peut remarquer que:
Phi^2=phi + 1
Donc phi^3=phi^2 x phi
=2phi + 1

Bonjour Lostounet, petite rectification du 31 !

par **totor60** » 31 Déc 2015, 12:34

j'ai fait le calcul ainsi : phi^2 + phi et j'ai trouvé le bon resultat !

Calculer phi a cube

Calculer phi a cube

Qui est en ligne