Equation + Nombre phi, 2nd.

par **Anonyme** » 30 Jan 2013, 14:28

1) Dans le même repère orthonormé (unité minimale 1cm) dessiner la droite D d'équation y = x-1 et l'hyperbole (H) d'équation y = 1/x

2) (D) et (H) se coupent en deux points. On note A celui dont l'abscisse est positive et cette abscisse est-elle même noté ;) (phi). Donner une valeur décimale approchée de ;).

3) Justifier que ;) est une solution de l'équation (e) = x²-x-1 = 0

4) Vérifier que (e) est équivalente à (x-1/2)²-5/4 = 0

5) Résoudre cette dernière équation et donner la valeur exacte du nombre ;) qui est appelé le "nombre d'or).

Beaucoup de mal avec les équations alors en plus avec ce nombre phi la dedans c'est galère. :mur:
De l'aide serait la bienvenue ! :S

par **XENSECP** » 30 Jan 2013, 14:37

Salut louloute, tu en es où ? :)

par **mcar0nd** » 30 Jan 2013, 14:39

Bonjour, la question 1 est quand même facile, pour la question, il te suffit de faire une lecture graphique.

Pour la 3, dire que les courbes D et H se coupent en un point ça signifie quoi? Quelle équation pourrais-tu poser pour "représenter" ça?

EDIT : J'arrive trop tard. :mur:

par **XENSECP** » 30 Jan 2013, 14:47

mcar0nd a écrit:EDIT : J'arrive trop tard. :mur:

Non pas vraiment. J'attends de voir ce qui a été fait avant de réagir donc j'ouvre le sujet (tu peux même le gérer si tu veux car il me parait trop simple pour moi).

par **Anonyme** » 30 Jan 2013, 14:47

XENSECP : Bonjour, j'ai fait les questions 1 et 2, je bloque avec le nombre phi. --'

mcar0nd : Bonjour, j'ai pas très bien compris votre répondre pour la question 3 :S

par **XENSECP** » 30 Jan 2013, 14:48

La question 3 c'est juste écrire sous forme demandée l'équation de la question 2 (équation qui dit que les 2 courbes se croisent).

par **mcar0nd** » 30 Jan 2013, 14:49

36-louloute a écrit:XENSECP : Bonjour, j'ai fait la question 3, je bloque avec le nombre phi. --'

mcar0nd : Bonjour, j'ai pas très bien compris votre répondre pour la question 3 :S

Si tu as fais la question 3 alors c'est parfait.

Si je comprends bien, tu es arrêté à la 4)?

par **mcar0nd** » 30 Jan 2013, 14:51

XENSECP a écrit:Non pas vraiment. J'attends de voir ce qui a été fait avant de réagir donc j'ouvre le sujet (tu peux même le gérer si tu veux car il me parait trop simple pour moi).

Ok, je veux bien terminer d'aider louloute alors si ça ne te dérange pas.

par **Anonyme** » 30 Jan 2013, 14:52

Non, erreur dans la réponse, désolé.
Comment peut-on trouver les solutions de (e) ? --'

par **XENSECP** » 30 Jan 2013, 14:52

36-louloute a écrit:Comment peut-on trouver les solutions de (e) ? --'

C'est genre la question 5 ça non ?

par **Anonyme** » 30 Jan 2013, 14:54

Ben non mais "justifier que phi est solution de (e)" ! --'

par **mcar0nd** » 30 Jan 2013, 14:57

36-louloute a écrit:Ben non mais "justifier que phi est solution de (e)" ! --'

En fait, on te dit que les courbes se coupent en un point qui est noté

, quelles est l'équation qui décrit le fait que les courbes se coupent en un point?

par **Anonyme** » 30 Jan 2013, 15:14

(D) coupe (H)
x-1 = 1/x
x-1-1/x=0
x(x-1-1/x)=0
x²-x-x/x=0
x²-x-1=0
Donc phi est une solution de phi.

C'est ça ? Sinon je vois pas comment faire..

par **mcar0nd** » 30 Jan 2013, 15:17

36-louloute a écrit:(D) coupe (H)
x-1 = 1/x
x-1-1/x=0
x(x-1-1/x)=0
x²-x-x/x=0
x²-x-1=0
Donc phi est une solution de phi.

C'est ça ? Sinon je vois pas comment faire..

Alors c'est pas évident de comprendre sans les balises TEX.
Mais c'est juste jusqu'à la 2éme ligne. Tu as donc

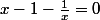
et ensuite tu mets tout au même dénominateur.

par **XENSECP** » 30 Jan 2013, 15:19

mcar0nd a écrit:Alors c'est pas évident de comprendre sans les balises TEX.
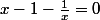
Mais c'est juste jusqu'à la 2éme ligne. Tu as donc et ensuite tu mets tout au même dénominateur.

Elle a tout multiplié par x, ce qui n'est pas faux non plus puisqu'on suppose que x est différent de 0 (sinon on pourrait pas utiliser 1/x).

par **mcar0nd** » 30 Jan 2013, 15:22

XENSECP a écrit:Elle a tout multiplié par x, ce qui n'est pas faux non plus puisqu'on suppose que x est différent de 0 (sinon on pourrait pas utiliser 1/x).

Ouais, c'est vrai j'avais pas fait attention... Autant pour moi.

par **Anonyme** » 30 Jan 2013, 15:36

Hmmm désolé je sais pas comment ça marche les balises TEX ! aha. :/

x(*x)/1 - 1*x/1 - 1/x*x = x*0
x² - x -x/x = 0
x²-x-1 = 0

C'est ça ? :S

par **Anonyme** » 30 Jan 2013, 15:54

Sinon pour la 4 j'ai fait :

(x-1/2)² - 5/4 = 0
x²-x+1/4-5/4
x²-x-1 = 0
x²-x-1 = 0

C'est bon ou non ?

par **mcar0nd** » 30 Jan 2013, 16:05

36-louloute a écrit:Sinon pour la 4 j'ai fait :

(x-1/2)² - 5/4 = 0
x²-x+1/4-5/4
x²-x-1 = 0
x²-x-1 = 0

C'est bon ou non ?

Oui c'est bon, juste c'est pas la peine de mettre =0 à chaque fois.
Pour la dernière question, il faut que tu factorise pour te ramener une équation de produits nuls.

par **Anonyme** » 30 Jan 2013, 16:08

Et donc la 3 c'est bon ?

Pour le 5 je dois résoudre l'équation ?

Equation + Nombre phi, 2nd.

Equation + Nombre phi, 2nd.

Qui est en ligne