Bonsoir tout le monde !
Je n'arrive pas à calculer cette limite en zéro :
(Exp(x)-x-1)/x² ?
Sur le graphe,ça donne un demi mais je n'y arrive pas à la calculer !
Merci :we:
Calcul d'une limite !
5 messages
- Page 1 sur 1
Shodix a écrit:Bonsoir tout le monde !
Je n'arrive pas à calculer cette limite en zéro :
(Exp(x)-x-1)/x² ?
Sur le graphe,ça donne un demi mais je n'y arrive pas à la calculer !
Merci :we:
Tu es en quelle classe ? Parce qu'avec les limites de références et théorème connus en terminale, je ne vois pas.
Sans les développement limités, il y a peut-être moyen, mais ce n'est en tout cas pas du niveau terminale. Si je ne me trompe pas... Ou alors il y a de la grosse astuce dans l'air !
Voici la méthode par développement limité, on remplace ici exp(x) par un polynôme (dév limité à l'ordre 2 en 0) avec ) une fonction qui tend vers 0 quand x tend vers 0.
une fonction qui tend vers 0 quand x tend vers 0.

-x-1}{x^2})
}{2x^2})
}{2})
Ainsi la limite pour x tend vers 0 donne 1/2.
A utiliser si tu as déjà vu les dév limité en cours, au moins le dév limité usuel de exp(x).
Ainsi la limite pour x tend vers 0 donne 1/2.
A utiliser si tu as déjà vu les dév limité en cours, au moins le dév limité usuel de exp(x).
Voici la méthode par développement limité, on remplace ici exp(x) par un polynôme (dév limité à l'ordre 2 en 0) avec ) une fonction qui tend vers 0 quand x tend vers 0.
une fonction qui tend vers 0 quand x tend vers 0.

-x-1}{x^2})
}{x^2})
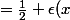)
Ainsi la limite pour x tend vers 0 donne 1/2.
A utiliser si tu as déjà vu les dév limité en cours, au moins le dév limité usuel de exp(x).
Ainsi la limite pour x tend vers 0 donne 1/2.
A utiliser si tu as déjà vu les dév limité en cours, au moins le dév limité usuel de exp(x).
Shodix a écrit:Bonsoir tout le monde !
Je n'arrive pas à calculer cette limite en zéro :
(Exp(x)-x-1)/x² ?
Sur le graphe,ça donne un demi mais je n'y arrive pas à la calculer !
Merci :we:
Rappel : Si f désigne une fonction dérivable en 0, alors une équation de la tangente à sa courbe représentative au point d'abscisse 0 est :
y=f'(0)x +f(0)
Attention : Je ne sais pas si ce que je vais dire est correct (et je ne sais même pas si ça existe), mais en s'inspirant de la formule qui donne l'équation d'une tangente à une courbe, on a qu'une équation de la parabole "tangente" à la courbe de l'exponentielle au point d'abscisse 0 est :
Du coup :
Je sais pas si on peut dire qu'une parabole peut-être "tangente" à une courbe (tangent sous-entend-il droite ?) et si c'est le cas, cela dépasse largement le cadre du lycée.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
