En ayant uniquement ces données, ces impossible : il nous faut une taille de référence (le stylo par exemple)
Pour t'expliquer : imagine qu'on prenne du même angle de vue une piscine, et que ces coins ont les mêmes coordonnées que tes points. Et bien cela voudrait dire que la piscine a la même taille que ta feuille !
Il nous faut donc la taille du stylo (et les coordonnées de ses deux bouts).
Si tu prend
)
le bout du stylo le plus haut et
)
le bout le plus bas, tu peux par la suite déterminer la longueur des vecteurs

et

en "unité" (vu que c'est une image je pense en pixels).
Tu calcules la longueur

en "pixels". Vu que tu connais la taille correspondante, il ne te reste plus qu'à faire un produit en croix.
MAIS cela restera une approximation car je néglige la perspective (on ne prends que 2 coordonnées (photo) alors que nous sommes dans l'espace)
Si tu veux être plus précis alors il faudrait beaucoup plus d'infos, pour pouvoir établir les 3 ème coordonnées de chaque points pour refaire la même chose mais dans l'espace.
EDIT :
Je prends un exemple :
)
)
Et


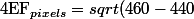^2+(30-200 )^2} = 10\times sqrt{293} pixels)
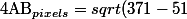^2+(30-102)^2} = 328 pixels)
Produit en croix :


De même ;

^2+(548-102)^2} \times 10} {10 \times sqrt{293}})

Je pense que c'est une feuille 21*29.7. Calculons les écarts relatifs :


De la même manière :

(désolé la lettre grecque "tau" ne fonctionne pas)
Donc même avec une approximation de la longueur du stylo (j'ai fait les coordonnées de E et F à vu de nez, et je ne connaissais pas la longueur du stylo) je retrouve les distances.
Refait la même chose avec les vraies mesures et tu trouveras surement un résultat bien meilleur.

