Résolution ... originale ?

par **upium666** » 26 Juil 2013, 03:05

Bonjour à tous et à toutes !

a)Déterminer une suite arithmétique (vn) qui satisfait la relation de récurrence (*)
b)On pose wn=un-vn. Montrer que cette suite établie est géométrique et préciser sa raison
c)Exprimer wn, puis un en fonction de n

J'aurais besoin de la première question uniquement
S'il vous plaît, détaillez vos démonstrations et énoncez une vérification

Merci

par **annick** » 26 Juil 2013, 06:42

Bonjour,
il me semble qu'il suffit d'écrire Un+1= Un + r (définition de la suite arithmétique), d'égaliser avec la formule de Un+1 que l'on te donne et de tenir compte de la valeur de U0 pour trouver r.

par **chan79** » 26 Juil 2013, 07:26

annick a écrit:Bonjour,
il me semble qu'il suffit d'écrire Un+1= Un + r (définition de la suite arithmétique), d'égaliser avec la formule de Un+1 que l'on te donne et de tenir compte de la valeur de U0 pour trouver r.

Bonjour
oui, on trouve r=4/3 et

=-16/9

par **upium666** » 27 Juil 2013, 16:57

chan79 a écrit:Bonjour
oui, on trouve r=4/3 et =-16/9

Vérification ?
Comment avez-vous fait ?

par **tototo** » 27 Juil 2013, 17:32

upium666 a écrit:Bonjour à tous et à toutes !

a)Déterminer une suite arithmétique (vn) qui satisfait la relation de récurrence (*)
b)On pose wn=un-vn. Montrer que cette suite établie est géométrique et préciser sa raison
c)Exprimer wn, puis un en fonction de n

J'aurais besoin de la première question uniquement
S'il vous plaît, détaillez vos démonstrations et énoncez une vérification

Merci

bonjour

comme u0=1
un=nr+1
un+1=1+(n+1)*r
1+(n+1)r=(1/4)(1+nr)+n=(1/4)+(1/4)*nr+n=1/4+n+(1/4)*n*r

par **chan79** » 27 Juil 2013, 17:42

upium666 a écrit:Vérification ?
Comment avez-vous fait ?

soit

il faut que, pour tout n,

l'dée est de regrouper les n

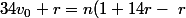Le membre de gauche et la quantité entre parenthèses doivent être nuls; c'est nécessaire pour que l'égalité soit vraie quel que soit n

Résolution ... originale ?

Résolution ... originale ?

Qui est en ligne