Calcul de limite en - l'infini
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nythostyle
- Membre Relatif
- Messages: 113
- Enregistré le: 22 Juil 2018, 17:17
-
 par nythostyle » 10 Juil 2020, 11:28
par nythostyle » 10 Juil 2020, 11:28
Bonjour, est ce que quelqu'un peut m'expliquer ou me renvoyer vers la théorie qui dit que pour des grandes valeurs négatives de x on peut procéder comme sur l'image ci dessous svp?
Merci !

-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 10 Juil 2020, 12:33
par Yezu » 10 Juil 2020, 12:33
Salut,
Si
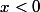
, alors
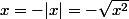
.
-
nythostyle
- Membre Relatif
- Messages: 113
- Enregistré le: 22 Juil 2018, 17:17
-
 par nythostyle » 12 Juil 2020, 17:54
par nythostyle » 12 Juil 2020, 17:54
Afin d'éviter de polluer le forum j'évite de créer un nouveau sujet et je pose une nouvelle question ici:

J'ai du mal à comprendre dans le deuxième point pourquoi il est dit que l'on choisit un delta inférieur à epsilon, étant donné que |f(x)|<ou=|x-1| que |x-1|< delta et que |f(x)|<epsilon, alors epsilon devrait être inférieur à delta? Quelqu'un saurait-il m'éclairer svp?
Merci !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 12 Juil 2020, 19:15
par Sa Majesté » 12 Juil 2020, 19:15
Salut,
En prenant
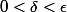
, tu as : pour tout x différent de 1, si
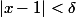
alors
| < |x-1| < \delta < \epsilon)
-
nythostyle
- Membre Relatif
- Messages: 113
- Enregistré le: 22 Juil 2018, 17:17
-
 par nythostyle » 15 Juil 2020, 15:32
par nythostyle » 15 Juil 2020, 15:32
Bonjour !
Alors j'ai vraiment l'impression de manquer quelque chose d'évident, mais quelqu'un sait il m'expliquer pourquoi 0 est exclu du domaine de définition? Je comprends que r=0 ne soit pas défini mais pas pour x

-
nythostyle
- Membre Relatif
- Messages: 113
- Enregistré le: 22 Juil 2018, 17:17
-
 par nythostyle » 15 Juil 2020, 15:38
par nythostyle » 15 Juil 2020, 15:38
nythostyle a écrit:Bonjour !
Alors j'ai vraiment l'impression de manquer quelque chose d'évident, mais quelqu'un sait il m'expliquer pourquoi 0 est exclu du domaine de définition? Je comprends que r=0 ne soit pas défini mais pas pour x

Serait-ce à cause de l'inclusion de [-3,3} dans [-|r|,[r|] ? dom f et les valeurs de r pour lesquelles l'expression a du sens sont désormais liés par relation d'inclusion?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Juil 2020, 11:59
par Ben314 » 16 Juil 2020, 11:59
Salut,
Pour que l'expression
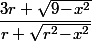
ait du sens, il faut que :
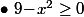
c'est à dire que
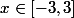
.
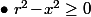
c'est à dire que
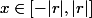
.
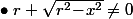
c'est à dire que, si
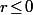
, on doit avoir
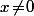
.
Par contre, si
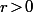
on peut parfaitement prendre
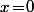
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités


