Besoin aide pour interprétation résultat limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 23 Jan 2017, 06:01
par novicemaths » 23 Jan 2017, 06:01
Bonjour
Voici une limite.
=\lim_{x \to +\infty} \frac{x^2+x+1}{x+1} = \lim_{x \to +\infty} \frac{x^2(1+\frac{1}{x}+\frac{1}{x^2})}{x(1+\frac{1}{x})} = \lim_{x \to +\infty} \frac{x(1+0+0)}{(1+0)} = \lim_{x \to +\infty} x=+\infty)
Est-ce que ce résultat indique que l'asymptote est situé en zéro de l'axe des abscisses ?
A bientôt

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 23 Jan 2017, 08:06
par capitaine nuggets » 23 Jan 2017, 08:06
Salut !
Je ne comprends pas trop ce que tu veux dire mais si ce sont des asymptotes que tu recherches, j'en vois deux :
- une asymptote verticale d'équation

car
| = + \infty)
et,
- une asymptote oblique d'équation
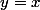
car tu peux remarquer que
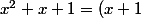x+1)
donc
-x = \frac{1}{x+1})
et ainsi
-x)=0)
.

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 23 Jan 2017, 12:33
par laetidom » 23 Jan 2017, 12:33
novicemaths a écrit:Bonjour
Voici une limite.
=\lim_{x \to +\infty} \frac{x^2+x+1}{x+1} = \lim_{x \to +\infty} \frac{x^2(1+\frac{1}{x}+\frac{1}{x^2})}{x(1+\frac{1}{x})} = \lim_{x \to +\infty} \frac{x(1+0+0)}{(1+0)} = \lim_{x \to +\infty} x=+\infty)
Est-ce que ce résultat indique que l'asymptote est situé en zéro de l'axe des abscisses ?
A bientôt
Salut @ vous deux,
Novicemaths,
Ce résultat indique que
f(x) tend vers

quand x tend vers

et en plus vis-à-vis de x qui te reste après les simplifications, donc la
droite y = x (la démonstration étant celle de capitaine nuggets - asymptote oblique -) :

donc
cette limite indique l'asymptote y = x
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 24 Jan 2017, 07:45
par novicemaths » 24 Jan 2017, 07:45
Bonjour
Ca ne va pas être facile de tracer les courbes à la main.
Merci pour vos lumières.
A bientôt

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 24 Jan 2017, 07:54
par laetidom » 24 Jan 2017, 07:54
novicemaths a écrit:Bonjour
Ca ne va pas être facile de tracer les courbes à la main.
Merci pour vos lumières.
A bientôt
Bonjour novicemaths !
Contents d'avoir été utile !
Et bien le fait de faire une étude de fonction conduisant à un tableau de variations complètement renseigné te permet en quelques secondes avec l'habitude de tracer
à la main l'allure de la courbe représentative de la fonction ! Idéal pour observer le comportement d'une fonction en un coup d'œil (produire un document synoptique peut être d'une grande utilité dans bien des configurations) ! :
Exemple :

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités

