Barycentre d'un quadrilataire quelconque

[matt075]

Bonsoir !

Voici un exercice que je dois faire il y a 2questions et je suis bloqué pour la 2eme...

ENONCE :
soit ABCD un quadrilatère quelconque dont les côtés sont régulièrement gradués (chaque côté divisé en trois tiers). Les graduations sont reliées comme sur la figure ci dessous pour obtenir le quadrilataire PQRS.



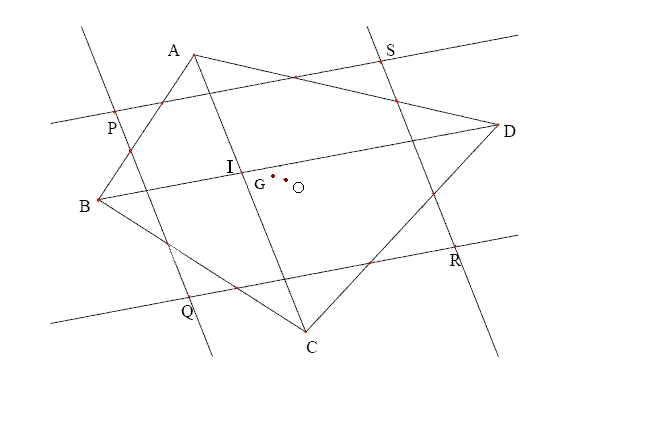
1° Montrer que PQRS est un parallélogramme
[pour cette question j'ai trouvé]

2° G est l'isobarycentre des points A, B, C et D
O est le centre du parallélogramme PQRS
I est le point d'intersection des diagonales [AC] et [BD]
Montrer que G, O et I sont alignés.

Là je ne sais vraiment pas comment faire, je suppose qu'il faut prouver que G est le barycentre de O et I ??

Merci d'avance pour votre aide ! bonne soirée

[armor92]

Bonjour matt075,

G est le barycentre de ABCD s'exprime par la relation :
4 = + + + (1)

O est le centre du parallélogramme PQRS, donc O est barycentre de PQRS :
4 = + + + (2)

Il faut démontrer que est colinéaire à

Soit A' le point d'intersection de IA et de PS.
De même soit B' le point d'intersection de IB et de PQ, C' le point d'intersection de IC et de QR, D' le point d'intersection de ID et de RS.

Le principe est de démontrer que IA'PB' est un parallélogramme, donc = +

En utilisans le théorème de THALES, on doit pouvoir démontrer que :
= 2/3
De même
= 2/3
D'ou :
= 2/3( + )

De même on démontre :
= 2/3( + )
= 2/3( + )
= 2/3( + )

Finalement d'après (2)
4 = 4/3( + + + ) = 16/3

D'ou finalement :
= 4/3