Bonjour à tous, voila mon exercice :
Les points A et B sont deux points distincts. Réduire chacune des somme vectorielles en introduisants si nécessaire un barycentre bien choisi:
a) 2MA + MB
b) MA + MB
c) 3MA - 5MB
d) MA - MB
J'ai fait l'exerice:
2MA + MB= 2MA + (MA + AB) = 3 MB
MA + MB = MA + (MA + AB) = 2MA + AB= 2MB
3MA - 5MB= 3MA - 5(MA-AB) = -2MB
MA-MB= MA - (MA+AB)= AB
Est-ce bon?
Merci de vos réponses car franchement je ne suis pas sur de mon exercice.
Barycentre de deux points
10 messages
- Page 1 sur 1
Salut !
:hum: je crois que tu n'y est pas du tout :triste:
a) Tout d'abord, regarde la somme des coefficients, elle n'est pas nulle donc le barycentre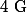 de ces point existe. Ensuite tu le définis en fonction des coefficient : Soit G le barycentre de (A,2),(B,1), pour tout point M du plan :
de ces point existe. Ensuite tu le définis en fonction des coefficient : Soit G le barycentre de (A,2),(B,1), pour tout point M du plan :
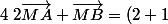\vec{MG}) .
.
Fais de même avec les autres :++:
:hum: je crois que tu n'y est pas du tout :triste:
a) Tout d'abord, regarde la somme des coefficients, elle n'est pas nulle donc le barycentre
Fais de même avec les autres :++:
Tu as parfaitement raison... de ne pas être sûr.KOnViCt a écrit:Merci de vos réponses car franchement je ne suis pas sur de mon exercice.
Prend une feuille, place au pif trois points A,B et M, regarde ou sont situés les vecteurs MA et MB et AB, puis trace quelque part sur la feuille les vecteurs 2MA+AB et 2MB.
FAIT LE puis dis moi si ces vecteurs sont égaux.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
A et B sont deux points du plan AB = 5
1) Construire le barycentre G de ( A, 2) (B , 3)
2) Determiner et tracer l'ensemble T des points M du plan tels que 2MA + 3MB = 10
3) Soit C un point n'appartenantpas à (AB). Determiner et tracer l'ensemble delta des points M tels que 2MA + 3MB soit colinéaire au vecteur AC.
La je sais vraiment pas quoi faire, pourriez-vous m'expliquer?
1) Construire le barycentre G de ( A, 2) (B , 3)
2) Determiner et tracer l'ensemble T des points M du plan tels que 2MA + 3MB = 10
3) Soit C un point n'appartenantpas à (AB). Determiner et tracer l'ensemble delta des points M tels que 2MA + 3MB soit colinéaire au vecteur AC.
La je sais vraiment pas quoi faire, pourriez-vous m'expliquer?
Pour la 2), je suppose que ton 2MA+3MB, ce sont des distances (et pas des vecteurs) et qu'elles ne sont pas au carré.
Dans ce cas, ça n'a pas grand chose à voir avec les barycentres et la solution est con-con ici : je te rapelle que le chemin le plus court entre deux points est la ligne droite, donc que MA+MB>(égal)AB=5 donc...
La 3) est trés facile... en utilisant la 1)
Dans ce cas, ça n'a pas grand chose à voir avec les barycentres et la solution est con-con ici : je te rapelle que le chemin le plus court entre deux points est la ligne droite, donc que MA+MB>(égal)AB=5 donc...
La 3) est trés facile... en utilisant la 1)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

