Arithmétique, TS,

par **souris bleue** » 29 Nov 2006, 13:36

Bonjour, je voudrais bien de l'aide pour les 2 exercices suivant. Je les ai trouvés dans un livre mais, il n'y a pas de correction. Je suis un peu perdu :cry:

Merci à vous de vien vouloir m'aider. :we: :++:

par **Elsa_toup** » 29 Nov 2006, 13:39

Bonjour,

C'est un peu long, alors on va procéder par étapes...
Pour la récurrence, il suffit d'appliquer le raisonnement.
Vérifie que c'est vrai pour

.
Puis on suppose que c'est vrai pour

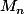
, et il reste à le montrer pour

.

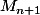
Où bloques-tu ?

par **souris bleue** » 01 Déc 2006, 20:17

:marteau: Désolé de ne pas l'avoir précisé, je viens de me rendre compte que je n'avais pas marquer ou je voulais de l'aide. :mur:

Pour l'exercice 1, je voudrais bien de l'aide pour les 2 dernières questions.
Et, pour l'exercice 2, je voudrais bien des pistes pour y arriver car, je ne comprends pas vraiment les questions, ce qu'il faut vraiment faire.
Désolé si je peux vous sembler un peu bête. :triste:

par **souris bleue** » 02 Déc 2006, 22:58

Finalement, je ne voudrais de l'aide plus que pour la question 3b et 4b pour l'exercice 1.
Et sinon, je n'ai réussi à faire que la première question de l'exercice 2. A croire que je suis vraiment nulle.
:stupid_in

par **Elsa_toup** » 02 Déc 2006, 23:23

Re,

Exercice 1.

3b).

, donc

.
Donc si,

non divisible par 3,

et

sont premiers entre eux.
bon c'est un peu sommaire...
Je laisse d'autres gens plus rigoureux que moi proposer une méthode plus rigoureuse.... :we:

.
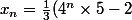Donc

, et est donc multiple de 3 ... (car

entier naturel)

par **Elsa_toup** » 02 Déc 2006, 23:31

Exercice 2.

2a). Si x et y sont tous deux pairs, on a :
(2k)²+(2k')² = 4k²+4k'² = 4(k²+k'²) = p².
Et donc p serait multiple de 2.

Si x et y sont tous deux impairs, on a:
(2k+1)²+(2k'+1)² = 4k²+4k+1+4k'²+4k'+1 = 4(k²+k'²+k+k') + 2 = 2 (2(k²+k'²+k+k')+1)
Bon là j'avoue je ne vois pas, mais je réfléchis...

par **souris bleue** » 02 Déc 2006, 23:41

Merci déjà de m'avoir aidé Elsa_toup, je vous laisse le temps de réfléchir car personellement, je suis bloquée :cry: :cry:, je reviendrais demain matin voir, si vous ou quelqu'un d'autre m'avez aidé et, je vous indiquerais également si j'ai trouvé quelque chose pour savoir si c'est juste car, normalement la nuit porte conseil. :dodo:
Et encore merci Elsa-toup de bien vouloir m'aider :salut:

par **Elsa_toup** » 02 Déc 2006, 23:42

Bonne nuit également (tu peux me tutoyer ... :happy2: )

par **souris bleue** » 03 Déc 2006, 11:48

Bonjour :we:
J'ai encore essayé de chercher pour l'exercice 2 mais, je cherche et je ne trouve pas.
Peux-tu encore m'aider Elsa_toup ou quelqu'un d'autre? :help:
Merci beaucoup :++:

Arithmétique, TS,

arithmétique, TS,

Qui est en ligne