Bonjour à tous,
Voilà j'ai un exercice de Maths à faire où je n'ai aucune idée du comment faire !! :triste:
C'est pour cela que je viens vous demander de l'aide pour que vous me donniez s'il vous plait quelques indices.
Voici l'exercice:
Créer un algorithme/programme permettant de faire afficher les 7 derniers chiffres de 7^2010.
D'avance merci,
Caroline.
[Seconde] Algorithme
13 messages
- Page 1 sur 1
Bonjour,
les 7 derniers chiffres d'un nombre , c'est son reste dans
la division euclidienne par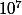
il se trouve que si l'on remplace un entier N par son reste r(N)
les choses marchent admirablement bien et tout est compatible
r(NM)=R(N)R(M)
r(N+M)=r(N)+R(M)
=r(r(N)^{2010}))
c'est ce que l'on appelle l'arithmétique modulaire, inventée par Gauss
il suffit de faire des multiplications et des exponentiations (élévations à la puissance) modulo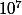
maintenant pour l'exposant 2010, le plus rapide est d'écrire 2010
en base 2
2010=1024+512+256+128+64+16+8+2
car^2=2^{2^{p+1}})
d'où
7^2
puis
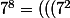^2)^2)
puis
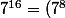^2)
ce qui donne l'algorithme modulo 10^7:
n=2010
x=7
faire tant que n > 1
si n est pair
x^2-->x (la base est élevée au carré)
n/2-->n (l'exposant est divisé par 2)
sinon
si n est impair
7*x-->x (la base est multipliée par 7)
n-1-->n (on soustrait 1 à l'exposant)
fin tant que
imprimer x (le résultat est x)
les 7 derniers chiffres d'un nombre , c'est son reste dans
la division euclidienne par
il se trouve que si l'on remplace un entier N par son reste r(N)
les choses marchent admirablement bien et tout est compatible
r(NM)=R(N)R(M)
r(N+M)=r(N)+R(M)
c'est ce que l'on appelle l'arithmétique modulaire, inventée par Gauss
il suffit de faire des multiplications et des exponentiations (élévations à la puissance) modulo
maintenant pour l'exposant 2010, le plus rapide est d'écrire 2010
en base 2
2010=1024+512+256+128+64+16+8+2
car
d'où
7^2
puis
puis
ce qui donne l'algorithme modulo 10^7:
n=2010
x=7
faire tant que n > 1
si n est pair
x^2-->x (la base est élevée au carré)
n/2-->n (l'exposant est divisé par 2)
sinon
si n est impair
7*x-->x (la base est multipliée par 7)
n-1-->n (on soustrait 1 à l'exposant)
fin tant que
imprimer x (le résultat est x)
mathelot a écrit:
ce qui donne l'algorithme modulo 10^7:
n=2010
x=7
faire tant que n > 1
si n est pair
x^2-->x (la base est élevée au carré)
n/2-->n (l'exposant est divisé par 2)
sinon
si n est impair
7*x-->x (la base est multipliée par 7)
n-1-->n (on soustrait 1 à l'exposant)
fin tant que
imprimer x (le résultat est x)
je m'étais un peu planté, je rectifie
n=2010 (l'exposant vaut 2010)
b=7 (la base vaut 7)
r=1 (on part d'un résultat qui vaut 1)
faire tant que n > 0
si n est pair
b^2-->b (la base est élevée au carré)
n/2-->n (l'exposant est divisé par 2)
sinon
si n est impair
b*r-->r
n-1-->n (on soustrait 1 à l'exposant)
fin tant que
imprimer r (le résultat est r)
J'ai essayé de le taper à la calculette mais ca ne fonctionne pas !
Et le problème c'est que la calculatrice (TI82 Stats) n'est pas capable de faire une telle puissance.
J4avais eu une idée qui était de prendre que les 7derniers chiffres puisqu'on a besoin que de ceux-ci mais le problème est que je ne sais pas comment le faire faire à la calculette :no:
Mais voici le début d'algorithme que j'ai fais:
Prompt N
For (P,10,2010)
N^P->R
If R>10000000
Then
...
Et c'est à ce moment là que je ne sais pas comment faire...
Si quelqu'un sait comment faire, pourriez vous m'aider s'il vous plait ?
Et le problème c'est que la calculatrice (TI82 Stats) n'est pas capable de faire une telle puissance.
J4avais eu une idée qui était de prendre que les 7derniers chiffres puisqu'on a besoin que de ceux-ci mais le problème est que je ne sais pas comment le faire faire à la calculette :no:
Mais voici le début d'algorithme que j'ai fais:
Prompt N
For (P,10,2010)
N^P->R
If R>10000000
Then
...
Et c'est à ce moment là que je ne sais pas comment faire...
Si quelqu'un sait comment faire, pourriez vous m'aider s'il vous plait ?
Carline a écrit:J'avais eu une idée qui était de prendre que les 7derniers chiffres puisqu'on a besoin que de ceux-ci mais le problème est que je ne sais pas comment le faire faire à la calculette :no:
remplacer un entier N par
N - int(N*10^(-7))*10^7
où int() est la partie entière
ça enlève à l'entier N, lui même privé de ses 7 chiffres de droite.
implémente l'algorithme que j'ai indiqué
- un (futur) résultat R
- un exposant N
- une base B
au départ ,
R vaut 1 (produit vide)
N vaut 2010,
B vaut 7
si l'exposant N est pair, on le divise par 2 et on remplace B par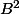
si l'exposant N est impair, on multiplie R par B (ce qui correspond
à transférer un seul facteur de
de  vers R) et on diminue l'exposant N de 1
vers R) et on diminue l'exposant N de 1
on fait ça jusqu'à que l'exposant N vaille zéro.
les calculs se font avec des entiers d'au plus 7 chiffres.
l'invariant de boucle (l'égalité qui reste vraie à chaque step du programme)
est

seulement au début R vaut 1. vaut
vaut
virtuellement (on n'effectue pas le calcul)
(on n'effectue pas le calcul)
Quant le programme se termine,c'est l'inverse. c'est qui vaut 1 , car N vaut zéro et R vaut réellement
qui vaut 1 , car N vaut zéro et R vaut réellement 
modulo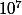
- un (futur) résultat R
- un exposant N
- une base B
au départ ,
R vaut 1 (produit vide)
N vaut 2010,
B vaut 7
si l'exposant N est pair, on le divise par 2 et on remplace B par
si l'exposant N est impair, on multiplie R par B (ce qui correspond
à transférer un seul facteur
on fait ça jusqu'à que l'exposant N vaille zéro.
les calculs se font avec des entiers d'au plus 7 chiffres.
l'invariant de boucle (l'égalité qui reste vraie à chaque step du programme)
est
seulement au début R vaut 1.
virtuellement
Quant le programme se termine,c'est l'inverse. c'est
modulo
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
