1ère - Produit Scalaire- Droite d'Euler d'un Triangle.

[Sophie586]

Bonjour, bonsoir hier j'ai reçu un exercice qui sera sans doute noté pour lundi, mais j'ai beau chercher une solution dans mes cours je ne sais pas comment faire pour résoudre cet exercice, merci d'avance.
L'exercice :

Lorsque j'écris --> c'est pour représenter la flèche d'un vecteur.

Soit ABC un triangle non équilatéral. On désigne par O le centre du cercle circonscrit à ce triangle. On note A', B' et C' les milieux respectifs des côtés [BC], [AC], [AB].



1. Soit G le point tel que GA--> + GB--> + GC--> = 0-->
a. Montrer que GA--> + 2GA'--> = 0-->. En déduire que les points G, A et A' sont alignés.
b. Démontrer de même que G, B et B' sont alignés.
c. En déduire que G est le centre de gravité du triangle ABC.

2. Soit H le point tel que OA--> + OB--> + OC--> = OH-->.
a. Montrer que AH--> = 20A'-->. EN déduire que la droite (AH) est perpendiculaire au côté [BC].
b. Montrer que H est l'orthocentre du triangle ABC.

3. Montrer que OH--> = 3OG-->. Que peut-on en déduire pour les points O, G et H ?

[capitaine nuggets]

Salut !

1)a) Tu sais que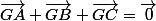 et tu veux obtenir . Pour cela, il faut justifier que , c'est-à-dire qu'il faut que tu montres que .
b) Même méthode, donne une égalité vectorielle semblable à celle qu'on t'a donné pour la question précédente : , qui permette d'affirmer directement que et 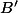sont alignés.