Bonjour , j'ai un petit soucis dans cet exercice de math ( premiere S )
Soit C la courbe representative de la fonction f définie sur R par :
[f(x)=x3] x3 = xcube
1) a)
Déterminer une équation de la tangente à la courbe "C" au point A d'abscice -2
b) montrer que cette tangente recoupe la courbe C en un point B dont on déterminera les coordonnés
c) Déterminer une équation de la tangente en B à la courbe C
Montrer que cette tangente recoupe C en un point E dont on déterminera les coordonnés.
2) Le point A est desormais comme abscisse A recoupe t'elle toujours C ?
Je ne comprend pas comment on resout ceci , il conclut une série de 4 ex , qui etait tous un peu bizarre sur ce meme chapitre et la je reste aveuglé !
Si vous avez une petite idée ...
Merci
1Ere S nb dérivé d'un fonction
6 messages
- Page 1 sur 1
par bernie » 09 Jan 2006, 14:22
Bonjour,
[f(x)=x3] x3 = xcube
1) a)
Déterminer une équation de la tangente à la courbe "C" au point A d'abscice -2
Tu dois savoir PAR COEUR que l'équa d'une tgte en 1 point d'abscisse"a" est:
y= f ' (a) (x-a)+f(a) (1)
f(-2)=-8
f '(x)=3x² donc f '(-2)=3(-2)²=12
équa tgte : y=12(x-(-2))-8=12x+16
b) montrer que cette tangente recoupe la courbe C en un point B dont on déterminera les coordonnés
Les abscisse des points d'intersec sont données par :
x^3=12x+16
soit x^3-12x-16=0 dont on sait qu'une racine double(car la droite est tgte) est x=-2 donc on met (x+2)² en facteur :
(x^3-12x-16)=(x+2)²(ax+b) --->on développe à droite pour comparer avec la gauche : VOIR PLUS BAS CE PASSAGE MODIFIE.
donc (x^3-12x-16)=(x+2)²(x-4)
donc il faut :(x+2)²(x-4) =0
Le 2ème point est x=4 dont le y est donné par x^3. B(4;?)
c) Déterminer une équation de la tangente en B à la courbe C
Montrer que cette tangente recoupe C en un point E dont on déterminera les coordonnés.
C'est le même travail. Tu appliques (1) avec a=4.
2) Le point A est desormais comme abscisse A recoupe t'elle toujours C ?
Cela n'est pas clair!!!!!!!
A+
[f(x)=x3] x3 = xcube
1) a)
Déterminer une équation de la tangente à la courbe "C" au point A d'abscice -2
Tu dois savoir PAR COEUR que l'équa d'une tgte en 1 point d'abscisse"a" est:
y= f ' (a) (x-a)+f(a) (1)
f(-2)=-8
f '(x)=3x² donc f '(-2)=3(-2)²=12
équa tgte : y=12(x-(-2))-8=12x+16
b) montrer que cette tangente recoupe la courbe C en un point B dont on déterminera les coordonnés
Les abscisse des points d'intersec sont données par :
x^3=12x+16
soit x^3-12x-16=0 dont on sait qu'une racine double(car la droite est tgte) est x=-2 donc on met (x+2)² en facteur :
(x^3-12x-16)=(x+2)²(ax+b) --->on développe à droite pour comparer avec la gauche : VOIR PLUS BAS CE PASSAGE MODIFIE.
donc (x^3-12x-16)=(x+2)²(x-4)
donc il faut :(x+2)²(x-4) =0
Le 2ème point est x=4 dont le y est donné par x^3. B(4;?)
c) Déterminer une équation de la tangente en B à la courbe C
Montrer que cette tangente recoupe C en un point E dont on déterminera les coordonnés.
C'est le même travail. Tu appliques (1) avec a=4.
2) Le point A est desormais comme abscisse A recoupe t'elle toujours C ?
Cela n'est pas clair!!!!!!!
A+
par bernie » 09 Jan 2006, 14:33
c) Déterminer une équation de la tangente en B à la courbe C
Montrer que cette tangente recoupe C en un point E dont on déterminera les coordonnés.
La tgte en B est y=48x-128
Tu écris ensuite :
x^3=48x-128
soit x^3-48x+128=0
mais on sait que x=4 est racine double donc :
x^3-48x+128=(x-4)²(ax+b)
Tu auras E(-8;?)
A+
Montrer que cette tangente recoupe C en un point E dont on déterminera les coordonnés.
La tgte en B est y=48x-128
Tu écris ensuite :
x^3=48x-128
soit x^3-48x+128=0
mais on sait que x=4 est racine double donc :
x^3-48x+128=(x-4)²(ax+b)
Tu auras E(-8;?)
A+
par bernie » 09 Jan 2006, 14:35
[quote="bernie"]Bonjour,
[f(x)=x3] x3 = xcube
1) a)
Déterminer une équation de la tangente à la courbe "C" au point A d'abscice -2
Tu dois savoir PAR COEUR que l'équa d'une tgte en 1 point d'abscisse"a" est:
y= f ' (a) (x-a)+f(a) (1)
f(-2)=-8
f '(x)=3x² donc f '(-2)=3(-2)²=12
équa tgte : y=12(x-(-2))-8=12x+16
b) montrer que cette tangente recoupe la courbe C en un point B dont on déterminera les coordonnés
Les abscisse des points d'intersec sont données par :
x^3=12x+16
soit x^3-12x-16=0 dont on sait qu'une racine double(car la droite est tgte) est x=-2 donc on met (x+2)² en facteur :
(x^3-12x-16)=(x+2)²(ax+b) --->on développe à droite pour comparer avec la gauche mais tu développes d'abord (x+2)² avant de le multiplier par (ax+b) :
donc on a : (x^3-12x-16)=(x+2)²(x-4)
donc il faut :(x+2)²(x-4) =0
Le 2ème point est x=4 dont le y est donné par x^3. B(4;?)
c) Déterminer une équation de la tangente en B à la courbe C
Montrer que cette tangente recoupe C en un point E dont on déterminera les coordonnés.
C'est le même travail. Tu appliques (1) avec a=4.
2) Le point A est desormais comme abscisse A recoupe t'elle toujours C ?
Cela n'est pas clair!!!!!!!
A+
[f(x)=x3] x3 = xcube
1) a)
Déterminer une équation de la tangente à la courbe "C" au point A d'abscice -2
Tu dois savoir PAR COEUR que l'équa d'une tgte en 1 point d'abscisse"a" est:
y= f ' (a) (x-a)+f(a) (1)
f(-2)=-8
f '(x)=3x² donc f '(-2)=3(-2)²=12
équa tgte : y=12(x-(-2))-8=12x+16
b) montrer que cette tangente recoupe la courbe C en un point B dont on déterminera les coordonnés
Les abscisse des points d'intersec sont données par :
x^3=12x+16
soit x^3-12x-16=0 dont on sait qu'une racine double(car la droite est tgte) est x=-2 donc on met (x+2)² en facteur :
(x^3-12x-16)=(x+2)²(ax+b) --->on développe à droite pour comparer avec la gauche mais tu développes d'abord (x+2)² avant de le multiplier par (ax+b) :
donc on a : (x^3-12x-16)=(x+2)²(x-4)
donc il faut :(x+2)²(x-4) =0
Le 2ème point est x=4 dont le y est donné par x^3. B(4;?)
c) Déterminer une équation de la tangente en B à la courbe C
Montrer que cette tangente recoupe C en un point E dont on déterminera les coordonnés.
C'est le même travail. Tu appliques (1) avec a=4.
2) Le point A est desormais comme abscisse A recoupe t'elle toujours C ?
Cela n'est pas clair!!!!!!!
A+
par Chimerade » 09 Jan 2006, 14:44
Bonjour,
Si f est dérivable en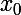
, l'équation de la tangente en 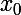à la courbe y=f(x) est :
}{x-x_0}=f'(x_0))
Ceci est vrai quelle que soit la fonction f ; c'est dans ton cours et tu devrais le savoir !
Par conséquent, l'équation donnant les intersections de la courbe C avec cette tangente est :
-f(x_0)}{x-x_0}=f'(x_0))
Dans le cas qui nous occupe=x^3)
, donc =3x^2)
L'équation de la tangente en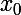 est donc :
et l'équation donnant les intersections avec C est donc :
Soit :
 = 3x_0^2\times (x-x_0))
Cette équation a pour racine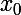 ; normal, la tangente passe bien par la courbe.
\times(x^2+xx_0+x_0^2)-3x_0^2\times (x-x_0) = 0)
\times(x^2+xx_0+x_0^2-3x_0^2) = 0)
\times(x^2+xx_0-2x_0^2) = 0)
Elle a même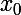 comme racine double ; normal puisque la tangente est tangente !
\times(x-x_0)\times(x+2x_0) = 0)
^2\times(x+2x_0) = 0)
Il est donc clair que la tangente à C en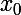 recoupe C en )
En fait, ceci résoud la question 2) mais tu n'as qu'à t'en inspirer pour résoudre les cas particuliers soulevés en 1)a), 1)b) et 1)c)
Si f est dérivable en
Ceci est vrai quelle que soit la fonction f ; c'est dans ton cours et tu devrais le savoir !
Par conséquent, l'équation donnant les intersections de la courbe C avec cette tangente est :
Dans le cas qui nous occupe
L'équation de la tangente en
et l'équation donnant les intersections avec C est donc :
Soit :
Cette équation a pour racine
Elle a même
Il est donc clair que la tangente à C en
En fait, ceci résoud la question 2) mais tu n'as qu'à t'en inspirer pour résoudre les cas particuliers soulevés en 1)a), 1)b) et 1)c)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :