Une pyramide à trois couleurs

par **Imod** » 14 Juin 2009, 17:27

Amis magiciens bonjour :+++:

Un petit tour de magie pour impressionner vos amis .

On demande à un membre du public d'aligner neuf jetons de couleur ( Bleu Jaune ou Rouge ) à l'abri du regard du magicien et d'annoncer la couleur du premier jeton qu'il a déposé ainsi que celle du jeton qu'il espère à l'issue des manipulations . Le magicien fournit alors un dixième jeton à déposer en bout de ligne et à la surprise générale le spectateur obtient la couleur voulue .

Les manipulations effectuées par le spectateur sont les suivantes : sous la première ligne il construit une deuxième ligne en plaçant un jeton de la troisième couleur entre deux jetons sont de couleurs différentes ou un jeton de la couleur commune entre deux jetons de même couleur . Il continue ainsi jusqu'à ce qu'il ne reste qu'un jeton qui doit être de la couleur demandée .

Une illustration avec une ligne de cinq jetons : le magicien ajoute le disque bleu et l'issue est un disque rouge .

Question subsidiaire : avec quels autres nombres de jetons le tour marche-t-il ?

Amusez-vous bien :zen:

Imod

par **Nightmare** » 14 Juin 2009, 17:39

Salut Imod :happy3:

Une question avant de m'y attaquer :
La couleur des jetons de la première ligne est-elle imposée au membre du public ou est-ce à sa guise?
Autrement dit, pour l'exemple des 9 jetons, les 9 jetons ont-ils une couleur prédéfinie ou le membre peut prendre n'importe lesquelles?

par **Nightmare** » 14 Juin 2009, 17:41

Ma question n'est toujours pas claire je crois, je recommence avec un exemple :

Le candidat doit il placer sur la première ligne par exemple 3 jetons de chaque couleurs ou peut-il placer 9 jetons de la même couleur ?

par **Imod** » 14 Juin 2009, 18:31

Seules les trois couleurs sont imposées le nombre de jetons de chaque couleur est libre , ont peut choisir uniquement des jaunes sur la première ligne , par exemple .

Imod

par **Doraki** » 14 Juin 2009, 18:56

Question subsidiaire : les puissances de 3.

par **Imod** » 14 Juin 2009, 20:38

Doraki a écrit:Question subsidiaire : les puissances de 3.

Oui , reste à donner la raison , ce n'est pas très difficile et plutôt amusant .

Imod

par **nodjim** » 15 Juin 2009, 16:13

Si je comprends bien, il faut démontrer que les règles qui régissent la couleur du jeton qu'on pose sous 2 autres s'applique aussi à l'ensemble du triangle?
Très fort :++:

par **Galax** » 17 Juin 2009, 10:46

Imod a écrit:Oui , reste à donner la raison , ce n'est pas très difficile et plutôt amusant .

Imod

Oui ca vient assez bien lorsqu'on voit que le jeton "fils" de A et B est en fait C=3-(A+B) (mod 3)

Du coup avec
A B C D
E F G
H I
J

on trouve facilement que J est le fils de A et D car les coefficients devant B et C sont alors multiples de 3 et s'annulent avec le (mod 3), ca se généralise donc dès que la premiere ligne comporte 3n+1 jetons.

Je ne suis pas sur d'avoir été très clair :hum:

par **Imod** » 17 Juin 2009, 14:39

Galax a écrit:Oui ca vient assez bien lorsqu'on voit que le jeton "fils" de A et B est en fait C=3-(A+B) (mod 3) ...

C'est la bonne méthode de calcul ou encore

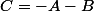
pour faire plus court :we:

Galax a écrit:Ca se généralise donc dès que la premiere ligne comporte 3n+1 jetons.

Essaie avec une première ligne : JBRJBRB :zen:

Imod

par **Galax** » 17 Juin 2009, 18:06

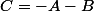
Imod a écrit:C'est la bonne méthode de calcul ou encore pour faire plus court :we:

Essaie avec une première ligne : JBRJBRB :zen:

Imod

3n+1 en comptant le jeton du magicien bien sur ... :doh:

par **Imod** » 17 Juin 2009, 21:17

Galax a écrit:3n+1 en comptant le jeton du magicien bien sur ... :doh:

C'est bien ce que j'avais compris . Comment le magicien avec la position JXXXXX va-t-il choisir le septième jeton pour trouver un rouge à la fin ?

Imod

par **Galax** » 18 Juin 2009, 08:35

Imod a écrit:C'est bien ce que j'avais compris . Comment le magicien avec la position JXXXXX va-t-il choisir le septième jeton pour trouver un rouge à la fin ?

Imod

Oui d'accord, ya un probleme :triste:

par **Galax** » 18 Juin 2009, 08:45

C'est en effet 3^n+1 et non pas 3n+1

par **Imod** » 18 Juin 2009, 21:37

Galax a écrit:C'est en effet 3^n+1 et non pas 3n+1

C'est ce qu'affirmait déjà Doraki mais sur un forum de maths on attend au moins l'idée de la démonstration :zen:
Pour neuf jetons plus un on peut le vérifier avec quelques petits calculs , mais pour le cas général ? Pourquoi les couleurs des jetons intermédiaires ( entre le premier et le dernier de la première ligne ) s'estompent-elles dans le résultat final ?

Imod

par **Galax** » 18 Juin 2009, 23:33

Imod a écrit:C'est ce qu'affirmait déjà Doraki mais sur un forum de maths on attend au moins l'idée de la démonstration :zen:
Pour neuf jetons plus un on peut le vérifier avec quelques petits calculs , mais pour le cas général ? Pourquoi les couleurs des jetons intermédiaires ( entre le premier et le dernier de la première ligne ) s'estompent-elles dans le résultat final ?

Imod

Il me semble (mais peut etre abuse-je) qu'à partir du moment où

1)

AxxB
xxx
xx
C

est equivalent à

2)

AB
C

passer de 2) à 1) revient à passer de 3^n+1 à 3^(n+1)+1
et la recurrence semble fonctionner ?

par **Imod** » 19 Juin 2009, 16:42

En effet ça marche :zen:

Et en toute rigueur :++:

Imod

Une pyramide à trois couleurs

Une pyramide à trois couleurs

Qui est en ligne