Test d'olympiade Morocco

[Will=?]

Partcicpez

[ffpower]

Désolé mais je préfererais éviter les torticolis..

[Olympus]

J'ai répondu au 1er, 2ème et 3ème . Le 4ème pas eu le temps par contre ( et je suis nul en géométrie de toute façon ^^ ) .

EDIT : en gros j'ai de quoi me qualifier pour la prochaine et dernière étape ^^

[Will=?]

Bonsoir
j'ai répondu pour 1 Et pour 2
pou 3 j'ai commis une grosse erreur 1\q<1/100 :mur:
(pouvez vous poster la solution de 3)

Lis mon message privé svp

[Olympus]

Pour le 3, je suis pas sûr mais j'ai essayé de donner un algo à ça sur un brouillon, puis j'ai traduit en suites ...

Première tentative de trouver le maximum de "p" et "q" :

T'as q<100, donc q<=99, donc

On a

Donc ( tirée d'une OIM de 1982~83 ça ? )

Donc .







Donc .

Deuxième tentative :







Donc

On essaie, comme on l'a fait à la première tentative, de trouver un nouveau maximum de grâce à ce .

On trouvera .
Donc .

Je fais une pause, je vais à la douche là ^^

[Ben314]

Pour ceux qui ont des problèmes de scoliose (dont je fait parti...)

[Olympus]

Je continue :

Tu auras compris le principe, on utilise le maximum de P précédent pour trouver le nouveau maximum de q, et utiliser ce dernier pour trouver un nouveau maximum de p .

Tu auras aussi remarqué que ces maximums peuvent s'exprimer par les deux suites récurrentes :

( avec ) .
et
.

Si on teste pour i=1, i=2, i=3, i=4, i=5 etc... On remarque qu'à partir du rang 2, le nombre 5 est retiré à q, et 1 est retiré à p .

Donc :

et .

On prouve cela par récurrence bien sûr .

Puis on met n=18 :

et

Ce qui veut dire qu'à la tentative n°20, on aura forcément .

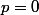
Or, on a , donc , ce qui est impossible .

[Ben314]

Pour le 3 :
=0,1982...
(2000-18)q10000p < (2000-17)q
17q < 2000(q-5p)18q
0 < 2000(q-5p) < 1800 ...

Pour le 4, si on connait les coordonnées barycentriques de O et de I (formules assez classiques) on s'en sort assez façilement

EDIT :
Pour l'exo 3, en regardant l'inégalité, on peut même dire "un peu mieux" en supposant q<222, la seule solution est 23/116=0,19827...

[manon_n]

Bonjour :happy2:

Est-ce que quelqu'un pourrait posté la correction du et du si ça vous gène pas ? Merci.

[Ben314]

Exo 1:
donc
Idem pour y et on en déduit que

qui, en développant donne le résultat.

Exo 2:
1) a>0 -> les variations de P sont : +oo ; décroissant ; croissant ; +oo
avec un minimum en -b/2a.

2) a-c>=0 et a-b+c>=0 -> 2a>=a+c>=b -> -b/2a>=-1
a-c>=0 et a+b+c>=0 -> 2a>=a+c>=-b -> -b/2a P s'annule donc en particulier P(-b/2a)=0 et P(1)=a+b+c>=0

Avec ça, on a les variations de P.

[benekire2]

Pour la 1 il devait pas y avoir 36 solutions .. mais j'ai fais légerement plus bourrin ( mais qui revient au même )

Une question pour Olympus ou des marocains ,

Comment se passe le "recrutement" pour les olympiades au maroc ?
Ca fait au moins 4 ou 5 étapes déjà .. et puis quelles sont les modalités pour accéder à l'étape suivante , si tu as un lien .. merci :zen:


PS: @Olympus : Je te dois toujours un résumé des exos abordés sur les transfos en 1S, je n'oubkie pas :we:

[kasmath]

il y'a des liens mais en arabe

[Olympus]

Ou alors poser a²=x-1 et b²=y-1 pour le premier, c'est plus "joli" ( pas de racines et tout ) ^^

@benekire2 : Je ne me souviens plus du nombre d'étapes qu'on a fait, mais à chaque fois y en a qui se font éliminer ( la team de notre lycée arrive toujours à tricher, sauf moi car je ne les y aide pas, donc elle n'a eu que 2 gars éliminés à la première étape ), ceux qui ne se font pas éliminer à la dernière étape, participeront l'année prochaine pour la selection d'une dizaine~vingtaine de candidats aux OIM .

Ces candidats seront formés dans un stage spécial à Rabat, avec bien sûr des éliminatoires afin de réduire leur nombre . Mais la qualité de la préparation n'est pas vraiment le top, et y a beaucoup beaucoup de copinage chez nous ( genre le fils du chef d'entreprise qui passe toujours alors qu'il ne bouge que rarement pendant les séances de maths ... ) ... ( cf. le score du Maroc aux OIM, no comment ) .

EDIT : ah ouais c'est la 5ème étape là .

[benekire2]

Merci beaucoup olympus :zen:

[benekire2]

Je viens de regarder les étapes 1,2 et 3 ; je trouve que le niveau n'est pas hyper progressif en fait. J'ai pas fait tout les exos, mais je trouve que c'est globalement le même niveau . Enfin ça n'engage que moi obv :zen:

[Olympus]

Ouép le niveau ne change pas, mais aux étapes 3 et 4 y avait pas d'inégalités si je me souviens bien ( combien j'avais ragé ce temps-là ^^ ) .

Ce sont les olympiades de TS qui me semblent plus intéressantes ...

[manon_n]

bonjour, est-ce que quelqu'un as su résoudre le quatrième exercice ?

Si oui comment fallait il faire ?

Je vous en remercie !

[Ben314]

Salut,
Dans un triangle quelconque ABC,
Le centre I du cercle inscrit est le barycentre de (A,sin) , (B,sin) , (C,sin)
Le centre O du cercle circonscrit est le barycentre de (A,sin) , (B,sin) , (C,sin)
Donc la droite (OI) coupe (AB) en M barycentre de (A,a) , (B,b) où
a = sinsin-sinsin = 2sinsin(cos-cos)
b = sinsin-sinsin = 2sinsin(cos-cos)
Donc M est sur le segment [AB] ssi (cos-cos) et (cos-cos) sont de même signe, c'est à dire ssi est le plus grand ou le plus petit des trois angles.

[sniperamine]

j'ai jamais su qu'il y avait un centre à rabat !!!

[manon_n]

Merci beaucoup ben314 !! Ca m'a éclairée :')