salut
le produit des chiffres vaut au maximum
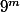
sinon c'est assez mal rédigée j'ai eu du mal à comprendre ce que voulais dire mais l'idée est bien là.
En re-rédigeant ce que tu as dit :
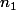
à
)
chiffres
A = {k tels que
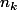
<
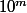
}
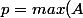)
alors

d'où
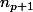
contient un '0' dans son écriture décimale
Tout n'est pas justifié : déja ton inégalité est fausse avec
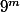
Il faut dire que tu suppose que
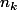
est non bornée pour justifier l'existence de p
Meme si ton inégalité est fausse, tu peux en trouver une similaire qui te permettra de conclure !
