
Suite bornée
6 messages
- Page 1 sur 1
Re: Suite bornée
Hello,
On coupe [0,2] en 2, puis encore en 2, etc, en prenant les trous au fur et à mesure :
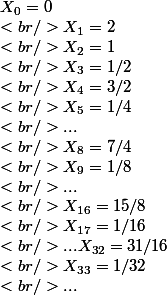
On a, en comparant Xi à n'importe quel Xj (j<i), toujours une distance superieure à (et égale à un multiple de) 1/2^n où 2^n est la puissance de 2 immediatement plus petite que i.
A fortiori,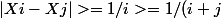)
L'expression étant symétrique en i,j, on peut laisser tomber la contrainte j<i.
Et voilà.
Edit: oups, il n'aime pas les line breaks \\ et je ne sais pas comment lui faire autrement
On coupe [0,2] en 2, puis encore en 2, etc, en prenant les trous au fur et à mesure :
On a, en comparant Xi à n'importe quel Xj (j<i), toujours une distance superieure à (et égale à un multiple de) 1/2^n où 2^n est la puissance de 2 immediatement plus petite que i.
A fortiori,
L'expression étant symétrique en i,j, on peut laisser tomber la contrainte j<i.
Et voilà.
Edit: oups, il n'aime pas les line breaks \\ et je ne sais pas comment lui faire autrement
Re: Suite bornée
Sans une définition formelle/claire de la suite  , j'ai du mal à accepter ce que tu affirmes
, j'ai du mal à accepter ce que tu affirmes 

Re: Suite bornée
Si il n'y a que ça
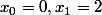
et
+1}{2^n})
qui est la même chose.
De là facile de voir que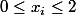 .
.
Et que x_i dans la tranche correspondant à n est de la forme (2*j+1)/2^n ie 'impair' / 2^n.
Pour j<i, s'il tombe dans la même tranche 'n', il est distant d'au moins 2 / 2^n de x_i.
S'il est dans une tranche plus basse p=n-k, alors x_j s'ecrit sous la forme}{2^p }= \frac{2^k (2l+1)}{2^n}) ie 'pair'/2^n et donc distant de x_i d'au moins 1/2^n.
ie 'pair'/2^n et donc distant de x_i d'au moins 1/2^n.
et comme 2^n < i, on raccroche les wagons du premier message.
Mieux ?
et
qui est la même chose.
De là facile de voir que
Et que x_i dans la tranche correspondant à n est de la forme (2*j+1)/2^n ie 'impair' / 2^n.
Pour j<i, s'il tombe dans la même tranche 'n', il est distant d'au moins 2 / 2^n de x_i.
S'il est dans une tranche plus basse p=n-k, alors x_j s'ecrit sous la forme
et comme 2^n < i, on raccroche les wagons du premier message.
Mieux ?
Re: Suite bornée
Oui c'est ok maintenant, super.
C'est peut être plus simple d'écrire :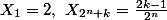 avec
avec  .
.
Dans ce cas le diamètre de la suite est 2. On peut montrer assez facilement que les suites qui vérifient l'énoncé doivent avoir un diamètre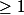
Mais on ne connait pas quelle est la borne inférieure de ce diamètre !
C'est peut être plus simple d'écrire :
Dans ce cas le diamètre de la suite est 2. On peut montrer assez facilement que les suites qui vérifient l'énoncé doivent avoir un diamètre
Mais on ne connait pas quelle est la borne inférieure de ce diamètre !
Re: Suite bornée
et en effet on sent bien qu'il y a pas mal de mou pour faire plus dense, vu la contrainte largement plus forte que vérifie cette suite \right)}}>\frac{1}{max(i,j)}>\frac{1}{i+j})
Ca fait quelques années que je n'étais pas passé sur le forum, ça fait plaisir de dérouiller un peu les méninges !
Ca fait quelques années que je n'étais pas passé sur le forum, ça fait plaisir de dérouiller un peu les méninges !

6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
