bonjour,
si je dis: 1+2 = 3
4+5+6 = 7+8
9+10+11+12 = 13+14+15
peut on poursuivre et approuver cela a l'infini?
merçi
Somme termes
4 messages
- Page 1 sur 1
par Chimerade » 14 Oct 2005, 16:36
On part de la constatation que :
Tirage 1 : 1+2 = 3
Tirage 2 : 4+5+6 = 7+8
Tirage 3 : 9+10+11+12 = 13+14+15
Et on se pose la question : est-ce que ça va continuer longtemps ?
Au premier tirage on prend un groupe de 3 nombres entiers, à partir de 1, que lon sépare en deux parties : un groupe de 2 nombres et un groupe de 1 nombre
Au premier tirage on prend un groupe de 1+2*1 nombres entiers, à partir de 1, que lon sépare en deux parties : un groupe de 1+1 nombres et un groupe de 1 nombre
Au deuxième tirage on prend un groupe de 5 nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 3 nombres et un groupe de 2 nombres
Au deuxième tirage on prend un groupe de 1+2*2 nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 1+2 nombres et un groupe de 2 nombres
Au troisième tirage on prend un groupe de 7 nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 4 nombres et un groupe de 3 nombres
Au troisième tirage on prend un groupe de 1+2*3 nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 1+3 nombres et un groupe de 3 nombres
Nous sommes donc amenés à supposer quau n-ième tirage, on prend un groupe de 1+2*n nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 1+n nombres et un groupe de n nombres.
Au (k+1)-ième tirage, on va donc prendre un groupe de 2*(k+1)+1 nombres. Pour savoir quel est le premier de ces nombres, il suffit de faire la somme des nombres tirés aux premier, deuxième, ,k-ième tirage soit :
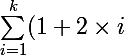 = k + 2\times (\sum_{i=1}^{k} (i)) = k+2\times \frac{k\times(k+1)}{2}=k+k\times (k+1)=k\times(k+2))
Le premier nombre sera donc :+1)
soit ^2)
Le premier groupe sera de longueur 1+(k+1) soit k+2 nombres ; il ira donc de à ^2+k+1)
. Sa somme sera donc : 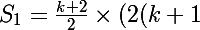^2+k+1)=\frac{(k+2)\times (k+1)\times (2k+3)}{2})
Le deuxième groupe sera de longueur (k+1) nombres ; il ira de^2+k+1+1)
à ^2+k+1+k+1)
. Sa somme sera donc : 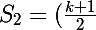((k+1)^2+k+1+1+(k+1)^2+k+1+k+1)=\frac{(k+1)\times(2*(k+1)^2+3k+4)}{2})
\times (2k^2+7k+6)}{2}=\frac{(k+1)\times (2k+3)\times (k+2)}{2}=S_1)
CQFD
Tirage 1 : 1+2 = 3
Tirage 2 : 4+5+6 = 7+8
Tirage 3 : 9+10+11+12 = 13+14+15
Et on se pose la question : est-ce que ça va continuer longtemps ?
Au premier tirage on prend un groupe de 3 nombres entiers, à partir de 1, que lon sépare en deux parties : un groupe de 2 nombres et un groupe de 1 nombre
Au premier tirage on prend un groupe de 1+2*1 nombres entiers, à partir de 1, que lon sépare en deux parties : un groupe de 1+1 nombres et un groupe de 1 nombre
Au deuxième tirage on prend un groupe de 5 nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 3 nombres et un groupe de 2 nombres
Au deuxième tirage on prend un groupe de 1+2*2 nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 1+2 nombres et un groupe de 2 nombres
Au troisième tirage on prend un groupe de 7 nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 4 nombres et un groupe de 3 nombres
Au troisième tirage on prend un groupe de 1+2*3 nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 1+3 nombres et un groupe de 3 nombres
Nous sommes donc amenés à supposer quau n-ième tirage, on prend un groupe de 1+2*n nombres entiers, à partir du premier entier non encore pris, que lon sépare en deux parties : un groupe de 1+n nombres et un groupe de n nombres.
Au (k+1)-ième tirage, on va donc prendre un groupe de 2*(k+1)+1 nombres. Pour savoir quel est le premier de ces nombres, il suffit de faire la somme des nombres tirés aux premier, deuxième, ,k-ième tirage soit :
Le premier nombre sera donc :
Le premier groupe sera de longueur 1+(k+1) soit k+2 nombres ; il ira donc de
Le deuxième groupe sera de longueur (k+1) nombres ; il ira de
CQFD
par Zebulon » 19 Nov 2005, 23:24
Bonsoir,
très joli problème et félicitations à Chimerade pour la solution!!!
C'est beau les Maths:se poser des questions... et en plus en trouver les solutions! :ptdr:
Zeb.
très joli problème et félicitations à Chimerade pour la solution!!!
C'est beau les Maths:se poser des questions... et en plus en trouver les solutions! :ptdr:
Zeb.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :