Somme des chiffres de n!
Olympiades mathématiques, énigmes et défis
-
khalilou
- Messages: 9
- Enregistré le: 07 Juin 2008, 11:36
-
 par khalilou » 13 Juin 2008, 17:16
par khalilou » 13 Juin 2008, 17:16
aviateurpilot a écrit:jcrois que pour montrer que cette limite tend vers l'infini,
il faut utiliser l'absurde,
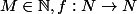
stict croissante tel que
!)\le M)
(evident)
a+
la fonction f représente koi ??
et s(f(n)!) est ce la somme des chifre ???
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 13 Juin 2008, 17:17
par Imod » 13 Juin 2008, 17:17
D'accord ainsi que pour l'autre remarque :we:
Imod
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 13 Juin 2008, 17:24
par aviateurpilot » 13 Juin 2008, 17:24
s( x)=somme des chiffre de x, ( n'est naturel)
on a partir d'un certain rang, f(n)! contien un nombre de chiffre qui ne depasse pa M. il donne forcement une contardiction apres un peu d'arithmetique (jvais voir apres)
khalilou )
est just une suite que j'ai construit (facile a faire mais l'important ici, c'est cmt l'utilisé)
jv'ai te montrer cment la conbstruire apres
-
khalilou
- Messages: 9
- Enregistré le: 07 Juin 2008, 11:36
-
 par khalilou » 13 Juin 2008, 17:58
par khalilou » 13 Juin 2008, 17:58
aviateurpilot a écrit:s( x)=somme des chiffre de x, ( n'est naturel)
on a partir d'un certain rang, f(n)! contien un nombre de chiffre qui ne depasse pa M. il donne forcement une contardiction apres un peu d'arithmetique (jvais voir apres)
khalilou )
est just une suite que j'ai construit (facile a faire mais l'important ici, c'est cmt l'utilisé)
jv'ai te montrer cment la conbstruire apres
g pa bien compri mon pote !!!!!
si c possible je ve des clarifications
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 13 Juin 2008, 20:07
par ffpower » 13 Juin 2008, 20:07
Ca a l air méchant comme exo.On peut essayer avec 2^n aussi..

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 05 Oct 2008, 16:18
par raito123 » 05 Oct 2008, 16:18
Salut,
Je tente une résolution :mlk:
On note S_n la somme de chiffre de n!
On a donc
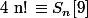
( 10 = 1 mod 9 ) d'où il existe un k>0 tq : n! = 9k + S_n d'ou S_n = n!-9k ,le passage au limite donne
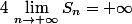
Et pour tout p dans IN on a p est congru S_p modulo 9 :happy2: !!
Les multiples ne doivent pas être utilisés sans nécessité
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 05 Oct 2008, 17:20
par miikou » 05 Oct 2008, 17:20
oula ! relis donc !!
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 07 Oct 2008, 15:08
par Doraki » 07 Oct 2008, 15:08
La somme des chiffres d'un multiple non nul de (10^n-1) est toujours supérieure ou égale à 9n.
Si on montre ça, le résultat en découle facilement.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 14 Oct 2008, 12:45
par kazeriahm » 14 Oct 2008, 12:45
raito123 a écrit:Salut,
Je tente une résolution :mlk:
On note S_n la somme de chiffre de n!
On a donc
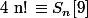
( 10 = 1 mod 9 ) d'où il existe un k>0 tq : n! = 9k + S_n d'ou S_n = n!-9k ,le passage au limite donne
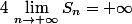
Et pour tout p dans IN on a p est congru S_p modulo 9 :happy2: !!
Salut,
bien tenté mais ca ne marche pas : ta démonstration reste la même que l'on considère n! ou toute autre fonction de n, notée f(n).
Tu montres donc que si f(n) tend vers l'infini alors la somme de ses chiffres aussi.
Ce qui est faux par exemple avec f(n)=10^n
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 26 Oct 2008, 09:00
par nodgim » 26 Oct 2008, 09:00
Supposons une limite à cette somme de chiffres, par exemple 10^10. Comme le nombre de chiffres de n! est aussi grand que l'on veut (même en ôtant les 0 à droite), quand il atteint 10^10, la valeur moyenne de chaque chiffre est 1. Quand n! (sans les 0 à droite) atteint 10^12 chiffres, il y a au moins 100 zéros pour un chiffre >=1.
Pourquoi, à partir d'un certain nombre, peut on admettre que les zéros vont devenir majoritaires ? Il faut remarquer qu'on atteint 10^12 chiffres pour n<<10^12, n étant plus près de 10^9. Quand il y a beaucoup de zéros, le multiplicateur vient les remplacer: 1000000000000000001*124567=124567000.....0000124567.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
stict croissante tel que
(evident)
est just une suite que j'ai construit (facile a faire mais l'important ici, c'est cmt l'utilisé)
( 10 = 1 mod 9 ) d'où il existe un k>0 tq : n! = 9k + S_n d'ou S_n = n!-9k ,le passage au limite donne