Somme des chiffres

[benekire2]

Bonsoir !

C'est assez inhabituel que je réfléchisse sur des olympiades, mais ce coup ci, je voulais absolument la faire, et comme je suis nul en arithmétique, je n'ai évidemment pas réussi à le montrer ni même avancé :triste:

Ca doit surement être facile, mais il y avait marqué "d'après olympiades" donc je le poste ici :


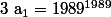
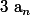
On pose et on pose la somme des chiffres de calculer

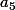
Si quelqu'un aurait la méthode , merci beaucoup !!

[Zweig]

Utilise le fait qu'un nombre est toujours congru à la somme de ses chiffres modulo 9.

[benekire2]

C'est aussi con que ça ? Parce que là on me demande d'exprimer a ; alors je vois pas trop ...

Merci beaucoup !

[Ben314]

Au cas où tu n'ais toujours pas trouvé, je rajouterais qu'il faut aussi utiliser le fait que la somme des chiffres de a est... beaucoup plus petit que a (quelle formule mathématique simple donne un majorant du nombre de chiffres de a ?) pour en déduire que a5 est petit (suffisement petit pour que la conaissance de son reste de division par 9 suffise à le connaitre...)

[benekire2]

ba en fait juste après avoir posté le message ( donc éteint le pc) j'ai montré que a5 possédait un seul et unique chiffre ( par les logarithmes) nb chiffres = E(log(n))+1

or 1989^1989=0[9] donc la somme des chifres de a1 est divisible par 9 d'où a5=9 est-ce ça ?
Merci.

[Zweig]

Je n'ai pas fait l'exercice, mais j'ai quelques doutes quand même sur la valeur trouvée ... a1 est quand même un trèsssss grand nombre, donc de là à arriver à avoir une somme d'un seul chiffres :hein:

[Ben314]

Le nombre de chiffre de a est effectivement 1+E(log(a)) qui est inférieur à 1+log(a) donc la somme des chiffres de a est inférieure à 9(1+log(a)).
si a1=1989^1989
alors a2<=9(1+1989*log(1989))<=59058
puis a3<=9(1+log(59058))<=52 (deux chiffres, le premier <=5)
donc a4<5+9=14

Comme 1989 est divisible par 9, a1 l'est aussi donc a2, a3 et a4 le sont et, comme ils sont non nuls, on a forcément a4=9

[benekire2]

@Zweig effectivement c'est un énorme nombre 1989^1989 mais le logarithme ma donné moins de 6000 chiffres donc au final ... itéré 5 fois on arrive sur un seul chiffre, sauf erreur bien sur.

Ben : Toi tu as fonctionné comme cela moi j'ai simplement dit que E(log(1989^1989))+1 =< E(1+log(10^(3*1989)))+1=<3*1989+2 mais ça reviens au même :zen: