Bonjour
Un ensemble E contient 2005 nombres entiers relatifs. A chaque élément de E, on associe la somme de tous les autres éléments de E et on obtient un ensemble F constitué lui aussi de 2005 nombres entiers relatifs. On observe que E et F sont identiques. Trouver le produit de tous les termes de E.
Bonne chance.
Le produit de 2005 nombres entiers
7 messages
- Page 1 sur 1
C'est malin...
Déjà, on ne peut pas facilement calculer le produit de 2005 nombres à moins de l'écrire sous la forme d'une puissance, il suffit cependant que parmis les 2005 nombres il y ait zéro pour connaître le résultat.
Pour prouver que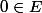 , il suffit de remarquer que si
, il suffit de remarquer que si 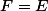 , alors
, alors  contient autant de nombres positifs que de nombres négatifs, et si
contient autant de nombres positifs que de nombres négatifs, et si 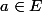 alors
alors 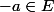 ,
, 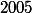 étant impair,
étant impair, 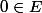 et les termes de E dans l'ordre croissant sont de la forme:
et les termes de E dans l'ordre croissant sont de la forme:
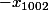 ,
, 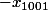 ...
... 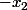 ,
, 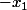 ,
,  ,
,  ,
,  ...
... 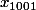 ,
, 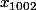
Déjà, on ne peut pas facilement calculer le produit de 2005 nombres à moins de l'écrire sous la forme d'une puissance, il suffit cependant que parmis les 2005 nombres il y ait zéro pour connaître le résultat.
Pour prouver que
C'ets bon je viens de retrouver la solution
Notons S la somme des éléments de E.
A un élément x de E, on associe lélément y de E tel que x + y = S.
Si S/2 nappartenait pas à E, on pourrait regrouper les éléments de E par paire ce qui contredirait le fait que Card(E) = 2005 impair.
Quitte à renuméroter les éléments, on peut supposer que E = {e1, , e2005} de manière à ce que ei + e2006-i = S pour tout i = 1..1003.
En particulier, en sommant cette égalité pour i=1..1003, on obtient S + e1003 = 1003S.
Sachant que 2*e1003 = S, on en déduit que S = e1003 = 0 et donc le produit des éléments de E est nul.
Notons S la somme des éléments de E.
A un élément x de E, on associe lélément y de E tel que x + y = S.
Si S/2 nappartenait pas à E, on pourrait regrouper les éléments de E par paire ce qui contredirait le fait que Card(E) = 2005 impair.
Quitte à renuméroter les éléments, on peut supposer que E = {e1, , e2005} de manière à ce que ei + e2006-i = S pour tout i = 1..1003.
En particulier, en sommant cette égalité pour i=1..1003, on obtient S + e1003 = 1003S.
Sachant que 2*e1003 = S, on en déduit que S = e1003 = 0 et donc le produit des éléments de E est nul.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
