Nombre de possibilités de recouvrir un damier n*2.

[Maks]

Bonsoir.
Une petite "énigme", avant de se coucher :

"Combien y-a-t'il de possiblités de recouvrir un damier grâce à des dominos (sans recouvrement, evidemment) ?"

Bon courage.

[Cheche]

Je dirais 2^n avec une démonstration très litigieuse.

[EDIT]
Mais après avoir fait quelques dessins, il est vrai que pour remplir un damier constitué d'un nombre impaire de case ; ça va être assez compliqué.

Bref, je suppose que le damier de 2*n veut dire un damier de 2*n sur 2*n.

[Maks]

Donne ta démonstration s'il te plaît.

[Maks]

Aaaaah !! Au temps pour moi !
Non, un damier représente, pour moi, un damier de longueur n et de hauteur 2. Si on prend un grand n, ca sera un loooooooong damier, en fait :id: !

Exemple
damier :
xxxxxxxxxx
xxxxxxxxxx

[nodjim]

C'est une suite de Fibonacci.
Si longueur n, le nombre de positionnements possibles est F(n+1).

[Maks]

Prouve-le.

[Cheche]

Ha lol, il est fun ton damier.

Début de Démonstration :

Propriété 1 :

Il est impossible que deux dominos horizontaux soient décaler d'une case.

ex : (les dominos sont représentés par des -)
00--000
000--00

ou
000--00
00--000

Démonstration de la propriété 1 :
On suppose la présence de deux dominos horizontaux décalés d'une case.

=> Ils séparent donc le damier en deux parties (celle de droite et celle de gauche) avec un nombre impaire de case, donc impossible à remplir.

=> la propriété 1 est donc vrai (raisonnement par l'absurde).

Propriété 2 :

Le damier 2*n est toujours constitué de deux figures :

Figure 1
00--00
00--00

et

Figure 2
00|00
00|00

D'après la propriété 1, la propriété 2 est vraie.

Conclusion :

Pour remplir un damier de taille 2*n, on prend le damier de taille 2*(n-2) auquel on rajoute la figure 1 et on prend le damier de taille 2*(n-1) auquel on rajoute la figure 2.


Nous avons donc une simple récurrence linéaire d'ordre deux.

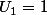
avec et

Après résolution, on trouve :

[Maks]

Ben c'est pas un damier de plouc ! J'attends ta démonstration !! Quand je vais te dire d'où viens l'exercice, tu rigoleras ... :ptdr:

[Zweig]

Ca doit venir d'un oral d'une ENS qui doit très certainement venir en fait d'un exercice d'Olympiade.

[Maks]

Exact. Mais honnêtement, cela n'est pas du niveau ENS. Enfin, disons que ce genre d'énoncé peut déstabiliser par son originalité, mais en soi ... si on raisonne calmement, je pense que c'est faisable.

[Clembou]

Prouve-le.

Hé oh !!! :hum: C'est à toi de faire la démonstration, nous donnons juste des indications ! Le message de Cheche devrait être hors régles...

[Maks]

Bonjour Clembou.
Excuse-moi, je ne comprends pas ton message. Je propose une énigme au forum, j'attends des tentatives de réponses ! Moi, je l'ai la solution. Je ne comprends pas ton problème. Explique-moi s'il te plaît.

De même, je ne vois pas en quoi le message de Cheche est "hors-règle" ...