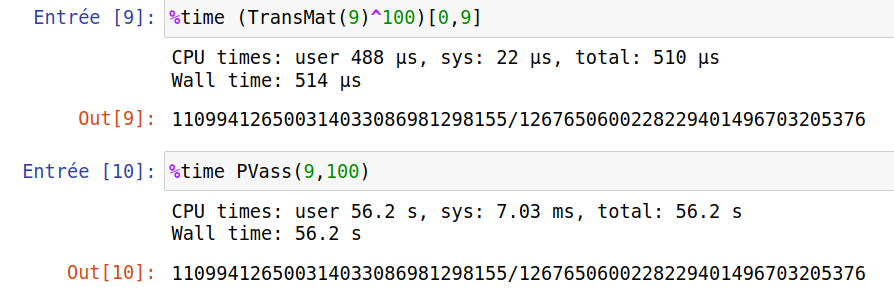
Joli code, ton esclave personnel se laisse convaincre en peu de lignes surtout sans formation préalable au calcul matriciel ! Je ne sais pas si je vais réussir à le persuader de se révolter en lui promettant une charge de travail moindre mais je lui propose :
Soit
)
la probabilité d'avoir au moins

faces successifs parmi

lancers
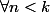
alors
=0)
pour
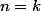
alors
=\frac{1}{2^k})
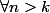
alors
 = P(k,n-1) + \frac{1}{2^{k+1}} (1-P(k,n-k-1)))
Ce n'est rien d'autre que l'idée de hdci un peu généralisée :
- soit j'ai une suite d'au moins

faces successifs dans les

premiers lancers donc proba
)
- soit je dois attendre les

derniers lancers pour avoir cette fameuse suite. Je finis par 1 pile puis

faces successifs donc proba
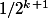
. Le tout après l'événement ne pas avoir eu au moins

faces successifs dans les
)
lancers précédents donc proba
)
Tu es d'accord avec mon calcul d’espérance de temps d'attente ? C'est surement trouvable aussi avec les matrices mais à première vue, cela m'a l'air plus pénible.
Pour la longueur de la plus grande suite, une équivalence en

peut-être ?