Martingale de l'excédent
martingale de l'excédent
Bonjour à tous et à toutes,
Je cherche à bien comprendre le fonctionnement de la martingale de l'excédent.
Pour le moement j'ai trouvé la description ici:
http://villemin.gerard.free.fr/Wwwgvmm/ ... leFace.htm
mais je trouve peu d'autres ref
Donc si vous avez:
des explications à donner
des refs à donner
d'autres mots clés pour avoir d'autres refs
Il ne s'agit pas de jouer , de l'utiliser.
Il s'agit d'en comprendre le principe.
Merci
Je cherche à bien comprendre le fonctionnement de la martingale de l'excédent.
Pour le moement j'ai trouvé la description ici:
http://villemin.gerard.free.fr/Wwwgvmm/ ... leFace.htm
mais je trouve peu d'autres ref
Donc si vous avez:
des explications à donner
des refs à donner
d'autres mots clés pour avoir d'autres refs
Il ne s'agit pas de jouer , de l'utiliser.
Il s'agit d'en comprendre le principe.
Merci
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: martingale de l'excédent
salut beagle,
je t'ai trouvé ça:
https://books.google.fr/books?id=EBErDw ... ce&f=false
donc principe de compensation semble autre mot clé pour des refs
et ce qui me fait rire c'est que l'on peut jouer l'inverse de la compensation.
autrement dit l'info historique , le passé de la série n'est pas le facteur qui intervient … si je comprends bien
je t'ai trouvé ça:
https://books.google.fr/books?id=EBErDw ... ce&f=false
donc principe de compensation semble autre mot clé pour des refs
et ce qui me fait rire c'est que l'on peut jouer l'inverse de la compensation.
autrement dit l'info historique , le passé de la série n'est pas le facteur qui intervient … si je comprends bien
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: martingale de l'excédent
Le passé de la série ne joue absolument pas, bien entendu.
C'est aussi un théorème qu'il est presque sûr que P-F passera une infinité de fois par 42 ... ou par -2019 ... ou par ce que tu veux.
C'est aussi un théorème qu'il est presque sûr que P-F passera une infinité de fois par 42 ... ou par -2019 ... ou par ce que tu veux.
Re: martingale de l'excédent
GaBuZoMeu a écrit:Le passé de la série ne joue absolument pas, bien entendu.
C'est aussi un théorème qu'il est presque sûr que P-F passera une infinité de fois par 42 ... ou par -2019 ... ou par ce que tu veux.
OK merci,
cela me rassure.
Je suis sur le site de Pierre avec des gens qui utilisent le retard pour augmenter les chances de gain dans le futur de la serie.
Et Ltav m'a mis ça dans les pattes.
Or j'y connais que couic en théorie des jeux et plein d'autres choses, cela m'a surpris un peu.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: martingale de l'excédent
Bonjour Beagle,
C'est une spécificité de Dlz que de défendre ce genre de théorie, c'est pour ça que cela avait frotté grave ici avec lui ! ( avec l'argument "puisque le pile n'est pas sorti depuis longtemps il va bien finir par sortir ..." : imparable)
Il faut avoir vu un joueur sortir ruiné du casino pour se méfier.... ( et on voit peu de casino faire faillite)
Mais d'une autre coté c'est tellement partagé.... au loto, en bourse ( je ne vais pas lancer le débat de savoir quel % de joueurs y croient !)
C'est une spécificité de Dlz que de défendre ce genre de théorie, c'est pour ça que cela avait frotté grave ici avec lui ! ( avec l'argument "puisque le pile n'est pas sorti depuis longtemps il va bien finir par sortir ..." : imparable)
Il faut avoir vu un joueur sortir ruiné du casino pour se méfier.... ( et on voit peu de casino faire faillite)
Mais d'une autre coté c'est tellement partagé.... au loto, en bourse ( je ne vais pas lancer le débat de savoir quel % de joueurs y croient !)
Re: martingale de l'excédent
Salut LeJeu ,
Pierre a été banni des différents forums de maths.
On n'est pas mieux servi que par soi-même , il a créé son site:
dlz9.forumactif.com/
Il y répète régulièrement que leJeu est un gars bien, un scientifique honnète,
bon jusque là je peux adhérer,
mais aussi que du temps de nuage sur maths forum, tu avais vérifié par tes propres tests que l'on pouvait gagner en jouant le retard au loto.Un truc genre décalage de 2% par rapport à jouer le hasard!
Alors ça je veux bien que tu nous rappelle cette vérification.
Il nous en parle régulièrement.
Pierre a été banni des différents forums de maths.
On n'est pas mieux servi que par soi-même , il a créé son site:
dlz9.forumactif.com/
Il y répète régulièrement que leJeu est un gars bien, un scientifique honnète,
bon jusque là je peux adhérer,
mais aussi que du temps de nuage sur maths forum, tu avais vérifié par tes propres tests que l'on pouvait gagner en jouant le retard au loto.Un truc genre décalage de 2% par rapport à jouer le hasard!
Alors ça je veux bien que tu nous rappelle cette vérification.
Il nous en parle régulièrement.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: martingale de l'excédent
Faisons une suite de 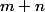 tirages à pile ou face. La probabilité d'avoir
tirages à pile ou face. La probabilité d'avoir 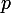 piles à l'issue de ces
piles à l'issue de ces 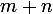 tirages est
tirages est 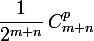 , tout le monde est d'accord là-dessus. C'est la loi binomiale.
, tout le monde est d'accord là-dessus. C'est la loi binomiale.
Maintenant, décomposons l'histoire : d'abord les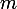 premiers tirages, puis les
premiers tirages, puis les  derniers.
derniers.
La probabilité d'avoir piles à l'issue des
piles à l'issue des 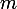 premiers tirages est
premiers tirages est  . Normalement, personne ne devrait avoir à redire à cela.
. Normalement, personne ne devrait avoir à redire à cela.
Quand on a déjà fait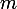 tirages, quelle que soit l'histoire précédente de la série de tirages, la probabilité d'avoir
tirages, quelle que soit l'histoire précédente de la série de tirages, la probabilité d'avoir 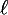 piles dans les
piles dans les  tirages qui suivent est toujours
tirages qui suivent est toujours 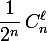 (même si au bout des
(même si au bout des 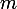 premiers tirages on avait 0 pile !). Ceci, même si ça chagrine les tenants du "rattrapage". La pièce est de mauvaise volonté, elle ne fait aucun effort pour rattraper son retard.
premiers tirages on avait 0 pile !). Ceci, même si ça chagrine les tenants du "rattrapage". La pièce est de mauvaise volonté, elle ne fait aucun effort pour rattraper son retard.
Mais bien qu'il n'y ait aucun rattrapage, la formule des probabilités totales nous dit que la probabilité d'obtenir en tout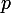 piles, quand on décompose l'histoire en deux morceaux, est
piles, quand on décompose l'histoire en deux morceaux, est
 = \dfrac1{2^{m+n}}\sum_{k+\ell=p} \left(C_m^{k}\times C_n^{\ell}\right) = \dfrac1{2^{m+n}}\, C_{m+n}^{p}\;,)
on retombe toujours bien sur la loi binomiale.
Je veux bien donner une démonstration de l'identité = C_{m+n}^{p}) à coup de bijection, pour faire plaisir à Beagle.
à coup de bijection, pour faire plaisir à Beagle.
Maintenant, décomposons l'histoire : d'abord les
La probabilité d'avoir
Quand on a déjà fait
Mais bien qu'il n'y ait aucun rattrapage, la formule des probabilités totales nous dit que la probabilité d'obtenir en tout
on retombe toujours bien sur la loi binomiale.
Je veux bien donner une démonstration de l'identité
Re: martingale de l'excédent
beagle a écrit:Salut LeJeu ,
Alors ça je veux bien que tu nous rappelle cette vérification.
Il nous en parle régulièrement.
J'ai retrouvé un fil intéressant de 2011, "Retard probabilité et statistiques" : Beagle ce n'est pas beau de vieillir... tu étais déjà dans la bagarre ( car c'était la bagarre...)
https://www.maths-forum.com/cafe-mathematique/retard-probabilite-statistiques-t117225-160.html ( page 9)
On y retrouve aussi tous les artistes de l'époque Nuage ,SkulKid, Fpower
J'y fais une contribution ou je réécris l'exemple qui fait controverse avec un nouveau générateur de nombre aléatoire ( Makoto Matsumoto and Takuji Nishimura) ,
Pour arriver à la conclusion , comme tout le monde, qu'il n'y a pas de retard, pas de passé...
Seul Dlz était en désaccord .
Re: martingale de l'excédent
ah, ok merci , je savais etre present à l'époque mais je ne me souviens plus de mes contributions.
et je ne retrouvais plus ce fil de discussion.
Sur les combinaisons je devais tenir la route mais sur les séries infinies j'ai du écrire des bétises à mon arrivée sur maths forum
effectivement nuage skullkid et ffpower étaient les cadors de l'époque ...
Je viens d'acheter le numéro de Pour la science sur le hasard.
Je vais pouvoir en parler avec Pierre et tout embrouiller encore plus!!!
On n' a pas fini...aie aie!
et je ne retrouvais plus ce fil de discussion.
Sur les combinaisons je devais tenir la route mais sur les séries infinies j'ai du écrire des bétises à mon arrivée sur maths forum
effectivement nuage skullkid et ffpower étaient les cadors de l'époque ...
Je viens d'acheter le numéro de Pour la science sur le hasard.
Je vais pouvoir en parler avec Pierre et tout embrouiller encore plus!!!
On n' a pas fini...aie aie!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: martingale de l'excédent
Petit exercice :
Au bout de 99 tirages, il y a 52 piles et 47 faces : pile est en avance de 5.
Quelle est, en fonction de n, la probabilité pour qu'au bout de n tirages supplémentaires se produise pour la première fois l'événement suivant :
1°) face rattrape son retard ;
2°) pile augmente son avance à 10 .
Au bout de 99 tirages, il y a 52 piles et 47 faces : pile est en avance de 5.
Quelle est, en fonction de n, la probabilité pour qu'au bout de n tirages supplémentaires se produise pour la première fois l'événement suivant :
1°) face rattrape son retard ;
2°) pile augmente son avance à 10 .
Re: martingale de l'excédent
On ne peut pas savoir, on a besoin de connaître plus précisément l'historique. On sait que Pile est en avance sur Face, mais tu ne dis pas si Pile vient de prendre de l'avance, ou si Pile était en avance au tout début, et l'écart est stable depuis les 40 ou 50 derniers tirages. Si par exemple, il y a eu 52 piles au début , et ensuite 47 faces, ou s'il y a eu alternativement 1 pile et 1 face depuis le début, avec quelques exceptions, l'impact sur la suite n'est pas le même.
Cette réponse, c'est la réponse que je devrais faire si je considérais que les tirages passés influent sur les tirages à venir. Bien entendu, c'est une grosse blague, et la probabilité est la même pour les 2 questions.
Cette réponse, c'est la réponse que je devrais faire si je considérais que les tirages passés influent sur les tirages à venir. Bien entendu, c'est une grosse blague, et la probabilité est la même pour les 2 questions.
Re: martingale de l'excédent
Ça c'est la partie évidente.
Mais que vaut cette probabilité ? Quelle est la loi de cette variable aléatoire n ? Et, question bonus, quelle est son espérance ?
Mais que vaut cette probabilité ? Quelle est la loi de cette variable aléatoire n ? Et, question bonus, quelle est son espérance ?
Re: martingale de l'excédent
La probabilité d'avoir exactement +5 ou -5 après n lancers, c'est quoi ?
Pour avoir +5 ou - 5,il faut déjà que n soit impair. sinon c'est impossible. Il faut aussi que n soit au moins égal à 5.
Si n est impair et au moins égal à 5, pour avoir +5, il faut avoir (n+5)/2 Piles et (n-5)/2 Face
Notons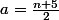 et
et 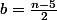
Avec ces notations :
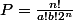
Pour avoir +5 ou - 5,il faut déjà que n soit impair. sinon c'est impossible. Il faut aussi que n soit au moins égal à 5.
Si n est impair et au moins égal à 5, pour avoir +5, il faut avoir (n+5)/2 Piles et (n-5)/2 Face
Notons
Avec ces notations :
Re: martingale de l'excédent
Ben non.
Je rappelle que la variable aléatoire n est le nombre de tirages supplémentaires pour que face rattrape son retard pour la première fois (ou que pile double son avance pour la première fois).
Je rappelle que la variable aléatoire n est le nombre de tirages supplémentaires pour que face rattrape son retard pour la première fois (ou que pile double son avance pour la première fois).
Re: martingale de l'excédent
Ahh ! J'aurais dû me douter que j'étais hors-sujet, c'était trop facile.
Exercice déjà vu ... je le laisse aux plus courageux que moi.
Exercice déjà vu ... je le laisse aux plus courageux que moi.
Re: martingale de l'excédent
Indication : principe de symétrie (ou de réflexion), plus la remarque qu'un chemin montant de 1 ou descendant de 1 à chaque étape qui part du niveau 0 et qui atteint pour la première fois le niveau 5 en 2k+1 étapes est au niveau 4 au bout de 2k étapes, sans avoir jamais passé au niveau 5.
Re: martingale de l'excédent
Un petit peu de simulation, avant de revenir à la théorie.
Je donne ci-dessous un petit code en Python3 pour produire une suite de "prem" tirages entre 0 et 1 avec retard de 0 égal à "ret" (de même parité que "prem"), puis effectuer ensuite "der" tirages (toujours même parité) pour voir si et quand il y a rattrapage du retard, ou doublement du retard.
Bien entendu, la première partie (faire "prem" tirages avec un retard fixé à "rem") ne sert absolument à rien. Mais il y a des gens qui s'imaginent que l'histoire des premiers tirages influe sur les derniers, sans se rendre compte que c'est contraire à l'hypothèse d'indépendance des tirages ...
Un exemple d'utilisation de la procédure :
retourne
Le premier quadruplet dit qu'il n'y a pas eu rattrapage, et qu'il y a eu doublement du retard au 73e tirage supplémentaire.
On regarde un peu ce qui se passe quand on fait varier le nombre de tirages supplémentaires :
sur 1000 essais :
487 rattrapages en au plus 51 tirages
492 doublement de retard en au plus 51 tirages
sur 1000 essais :
618 rattrapages en au plus 101 tirages
634 doublement de retard en au plus 101 tirages
sur 1000 essais :
693 rattrapages en au plus 151 tirages
660 doublement de retard en au plus 151 tirages
sur 1000 essais :
718 rattrapages en au plus 201 tirages
718 doublement de retard en au plus 201 tirages
sur 1000 essais :
757 rattrapages en au plus 251 tirages
753 doublement de retard en au plus 251 tirages
La dernière réponse, par exemple, est obtenue avec
On va pouvoir comparer avec les résultats théoriques.
Une chose déjà : ça illustre bien le fait qu'il n'y a aucun avantage à parier sur le rattrapage du retard par rapport au doublement du retard.
Je donne ci-dessous un petit code en Python3 pour produire une suite de "prem" tirages entre 0 et 1 avec retard de 0 égal à "ret" (de même parité que "prem"), puis effectuer ensuite "der" tirages (toujours même parité) pour voir si et quand il y a rattrapage du retard, ou doublement du retard.
- Code: Tout sélectionner
from random import *
def essai(prem,ret,der) :
# fait prem tirages entre 0 et 1,
# recommence jusqu'à ce que le retard de 0 sur 1
# soit égal à ret au bout des prem tirages
r=0
while r != ret :
r=0
for i in range(prem) :
if randrange(2)==0 : r-=1
else : r+=1
# après les prem tirages avec 0 en retard de ret,
# fait der autres tirages et renvoie
# rat : 1 si retard rattrapé, 0 sinon
# trat : nombre de tirages supplémentaires pour rattrapage
# dbl : 1 si doublement retard, 0 sinon
# tdbl : nombre de tirages supplémentaires pour doublement
rat=0; trat="NA"; dbl=0; tdbl="NA"
for j in range(der) :
if randrange(2)==0 : r-=1
else : r+=1
if rat==0 :
if r==0 :
trat=j+1 ; rat=1
if dbl==0 :
if r==2*ret :
tdbl=j+1 ; dbl=1
return rat,trat,dbl,tdbl
Bien entendu, la première partie (faire "prem" tirages avec un retard fixé à "rem") ne sert absolument à rien. Mais il y a des gens qui s'imaginent que l'histoire des premiers tirages influe sur les derniers, sans se rendre compte que c'est contraire à l'hypothèse d'indépendance des tirages ...
Un exemple d'utilisation de la procédure :
- Code: Tout sélectionner
for i in range(10) : print (essai(99,5,101))
retourne
- Code: Tout sélectionner
(0, 'NA', 1, 73)
(1, 21, 1, 57)
(0, 'NA', 1, 15)
(1, 59, 0, 'NA')
(1, 73, 1, 9)
(1, 17, 0, 'NA')
(1, 31, 1, 9)
(1, 23, 0, 'NA')
(1, 13, 0, 'NA')
(1, 33, 0, 'NA')
Le premier quadruplet dit qu'il n'y a pas eu rattrapage, et qu'il y a eu doublement du retard au 73e tirage supplémentaire.
On regarde un peu ce qui se passe quand on fait varier le nombre de tirages supplémentaires :
sur 1000 essais :
487 rattrapages en au plus 51 tirages
492 doublement de retard en au plus 51 tirages
sur 1000 essais :
618 rattrapages en au plus 101 tirages
634 doublement de retard en au plus 101 tirages
sur 1000 essais :
693 rattrapages en au plus 151 tirages
660 doublement de retard en au plus 151 tirages
sur 1000 essais :
718 rattrapages en au plus 201 tirages
718 doublement de retard en au plus 201 tirages
sur 1000 essais :
757 rattrapages en au plus 251 tirages
753 doublement de retard en au plus 251 tirages
La dernière réponse, par exemple, est obtenue avec
- Code: Tout sélectionner
n=251
L=[essai(99,5,n) for i in range(1000)]
print ("sur 1000 essais :")
print ([e[0] for e in L].count(1),\
"rattrapages en au plus", n, "tirages")
print ([e[2] for e in L].count(1),\
"doublement de retard en au plus", n, "tirages")
On va pouvoir comparer avec les résultats théoriques.
Une chose déjà : ça illustre bien le fait qu'il n'y a aucun avantage à parier sur le rattrapage du retard par rapport au doublement du retard.
Re: martingale de l'excédent
Revenons à la théorie.
On appelle la variable aléatoire qui est le nombre de tirages supplémentaires à effectuer pour arriver la première fois à ce que le nombre de faces rattrape son retard de 5. Comme les tirages supplémentaires sont indépendants des 99 tirages précédents,
la variable aléatoire qui est le nombre de tirages supplémentaires à effectuer pour arriver la première fois à ce que le nombre de faces rattrape son retard de 5. Comme les tirages supplémentaires sont indépendants des 99 tirages précédents,  est le nombre de tirages à effectuer pour que face soit en avance de 5 sur pile.
est le nombre de tirages à effectuer pour que face soit en avance de 5 sur pile.
Pour trouver la loi de , on va compter les chemins (montant ou descendant de 1 à chaque étape) partant de 0 et arrivant pour la première fois au niveau 5 au bout de
, on va compter les chemins (montant ou descendant de 1 à chaque étape) partant de 0 et arrivant pour la première fois au niveau 5 au bout de  étapes.
étapes.
Si est pair, aucun chemin. Si
est pair, aucun chemin. Si 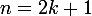 , un tel chemin sera au niveau 4 à l'étape
, un tel chemin sera au niveau 4 à l'étape 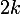 . On est donc amené à compter les chemins arrivant au niveau 4 au bout de
. On est donc amené à compter les chemins arrivant au niveau 4 au bout de 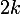 étapes sans jamais être passés par le niveau 5. En oubliant cette dernière contrainte, ça fait
étapes sans jamais être passés par le niveau 5. En oubliant cette dernière contrainte, ça fait 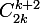 chemins. Mais il faut retirer de ça les mauvais chemins, ceux qui passent par le niveau 5. C'est ici qu'intervient le principe de symétrie : un tel mauvais chemin, on le modifie en prenant son symétrique par rapport à la droite
chemins. Mais il faut retirer de ça les mauvais chemins, ceux qui passent par le niveau 5. C'est ici qu'intervient le principe de symétrie : un tel mauvais chemin, on le modifie en prenant son symétrique par rapport à la droite 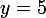 à partir du moment où le chemin touche cette droite. Sur le dessin, un mauvais chemin en rouge et la partie modifiée en vert.
à partir du moment où le chemin touche cette droite. Sur le dessin, un mauvais chemin en rouge et la partie modifiée en vert.
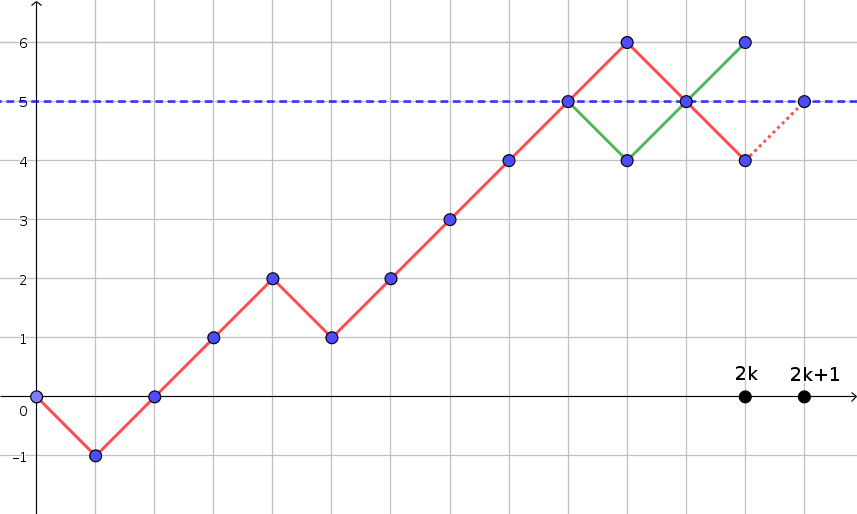
Indication ajoutée spécialement pour le charlatan de première, qui finira peut-être par comprendre le principe de réflexion : cette modification des mauvais chemins illustrée par le dessin réalise une bijection entre l'ensemble des mauvais chemins et l'ensemble de tous les chemins qui arrivent au niveau 6 en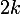 étapes. Le nombre de mauvais chemins est ainsi égal au nombre de chemins qui arrivent au niveau 6 au bout de
étapes. Le nombre de mauvais chemins est ainsi égal au nombre de chemins qui arrivent au niveau 6 au bout de 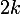 étapes et donc le nombre de bons chemins est
étapes et donc le nombre de bons chemins est
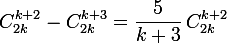
La loi de est donc donnée par
est donc donnée par =0) et
et =\dfrac{5}{(k+3)2^{2k+1}}\,C_{2k}^{k+2}) .
.
Prochain épisode : calcul de l'espérance de .
.
On appelle
Pour trouver la loi de
Si

Indication ajoutée spécialement pour le charlatan de première, qui finira peut-être par comprendre le principe de réflexion : cette modification des mauvais chemins illustrée par le dessin réalise une bijection entre l'ensemble des mauvais chemins et l'ensemble de tous les chemins qui arrivent au niveau 6 en
La loi de
Prochain épisode : calcul de l'espérance de
Modifié en dernier par GaBuZoMeu le 02 Jan 2020, 23:52, modifié 1 fois.
Re: martingale de l'excédent
Calculons l'espérance de la variable aléatoire  . C'est
. C'est
=\sum_{k\in \mathbb{N}} \dfrac{5(2k+1)}{(k+3)2^{2k+1}}\,C_{2k}^{k+2}\;.)
On peut trouver un équivalent simple du terme général de cette série grâce à la formule de Stirling.
}{(k+3)2^{2k+1}}\,C_{2k}^{k+2}\sim \dfrac{5}{2^{2k}}\,\dfrac{(2k)!}{(k!)^2}\sim \dfrac{5}{2^{2k}}\,\dfrac{\sqrt{4\pi k}(2k/e)^{2k}}{2\pi k(k/e)^{2k}}=\dfrac{5}{\sqrt{\pi}}\,\dfrac{1}{\sqrt{k}})
Cet équivalent est le terme général d'une série qui diverge vers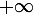 . Donc
. Donc =+\infty) . Troublant, non ? On a un événement qui se produit presque sûrement une infinité de fois, mais l'espérance du temps d'arrivée est infinie !
. Troublant, non ? On a un événement qui se produit presque sûrement une infinité de fois, mais l'espérance du temps d'arrivée est infinie !
De quoi porter un coup au moral des tenants de la martingale de l'excédent - sauf que ça leur en touche une sans faire bouger l'autre vu qu'ils ne comprennent pas grand chose aux probas.
Prochain et dernier épisode : confronter la théorie à la simulation.
On peut trouver un équivalent simple du terme général de cette série grâce à la formule de Stirling.
Cet équivalent est le terme général d'une série qui diverge vers
De quoi porter un coup au moral des tenants de la martingale de l'excédent - sauf que ça leur en touche une sans faire bouger l'autre vu qu'ils ne comprennent pas grand chose aux probas.
Prochain et dernier épisode : confronter la théorie à la simulation.
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
