Le jeu de dâmes

[Arescin]

Bonsoir, je propose une nouvelle énigme ( je ne l'ai pas aperçu ) sur le forum alors je me lance.

Vous possédez une piste de jeu de dame, donc de 8 x 8 cases.

Vous devez placer 8 pions de tel sorte que :
- Ils ne se croisent pas en diagonal.
- Ils ne se croisent pas en horizontal
- Ils ne se croisent pas en vertical

J'ai réussi à trouver une solution ( par hasard j'avoue :ptdr: )

[aviateurpilot]

Vous devez placer 8 pions de tel sorte que :
- Ils ne se croisent pas en diagonal.
- Ils ne se croisent pas en horizontal
- Ils ne se croisent pas en vertical

on suppose un repete
la place du pion est

ou est une permutation de
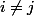
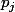
et quelque soit pour 2 pions et de {1,2,...,8}
c ça ce que tu veus dire?

[Arescin]

Vous devez placer 8 pions de tel sorte que :
- Ils ne se croisent pas en diagonal.
- Ils ne se croisent pas en horizontal
- Ils ne se croisent pas en vertical

on suppose un repete
la place du pion est

ou est une permutation de
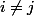
et quelque soit de {1,2,...,8}
c ça ce que tu veus dire?

En gros 2 pions ne peuvent pas être alignés verticalement, horizontalement, diagonalement

[Patastronch]

Ca s'appelle le probleme des 8 reines, comment placer 8 reines sans qu'elles se menacent sur un échequier.

[aviateurpilot]

En gros 2 pions ne peuvent pas être alignés verticalement, horizontalement, diagonalement

c'est que j'ai traduit mathématiquement

[Chimomo]

Sauf qu'il n'y a pas autant de cases sur un échiquier que sur un damier.

[Patastronch]

c'est que j'ai traduit mathématiquement

SOit j'ai pas compris ce que tu as écrit soit c'est completement faux.

[aviateurpilot]

soit tu n'as pas de niveau en math, soit tu ne comprend que les simple exo de programme.
essaye de comprendre ,si tu n'arrive pas , dis le moi pour que je t'explique

[BancH]

Arescin, peux-tu donner les coordonnées des emplacement des pions que tu as trouvées ?

[Patastronch]

[.../...]

Ca ne traduit pas toutes les contraintes selon moi. Un petit exemple ?

P1=(1,1) et P2=(2,1)

Ils sont pourtant sur la meme verticale. Donc c'est pour ca que je disais soit j'ai pas capté ce que tu as ecrit soit c est completement faux. Pour ca que je te demandais implicitement de m'expliquer ton truc et je m'attendais pas a que tu le prennes mal et que tu ais une réaction aussi pueril.

[Patastronch]

Arescin, peux-tu donner les coordonnées des emplacement des pions que tu as trouvées ?

Il y a (de mémoire donc a vérifier) 48 solutions en comptant les solutions similaires par rotation et par symétrie, soit 6 solutions vraiment distincte. Mais c est de mémoire donc c'est à vérifier.

[BancH]

ou est une permutation de

C'est ici qu'il est dit que chaque ordonnée est différente.

[Patastronch]

[edit]

Ok autant pour moi, prenons plutot P1=(1,2) et P2=(2,1) , ils sont sur la meme diagonale et tes contraintes n'empechent pas ces positionnements.

[Arescin]

x : y
x = vertical
y = horizontal

4:1
2:2
7:3
3:4
6:5
8:6
1:7
5:8

Un pote qui cherchait aussi m'a filé une astuce. Pour bien placer les points on peut s'aider des cavaliers aux échecs qui se déplacent en L sur 3 cases

[aviateurpilot]

dsl Patastronch
mais tt ce que j'ai fais est vrai
mai j'ai oublie le ca
4:1
2:2
7:3
3:4
6:5
8:6
1:7
5:8
verifie ce que j'ai fais

[mln]

Il y a 12 solutions distrinctes par transformations (rotations, symétries ) et 92 solutions en tout.

[Patastronch]

dsl Patastronch
mais tt ce que j'ai fais est vrai
mai j'ai oublie le ca

Ok la ca a l'air de marcher un peu mieu.

La prochaine fois essai juste de pas te la raconter quand on te demande de l'aide pour comprendre surtout quand c est réellement faux ... se relire, se planter ou faire des fautes d'innatention n'est pas une preuve de faiblesse intellectuelle.