Géométrie, demi-cercle inscrit dans un carré

[Thiéfaine]

Bonjour, j'ai un problème avec cette question:



Merci

[catamat]

Bonjour, une solution avec de la trigo...
Soit M le milieu de [AB]
les triangles DMA et DMQ sont isométriques donc DQ=DA=6
Soit a la mesure de l'angle on a tan(a)=

donc et

Soit h la hauteur du triangle grisé relative à la base [DC]
L'aire cherchée vaut 3h
et

Donc l'aire vaut

[catamat]

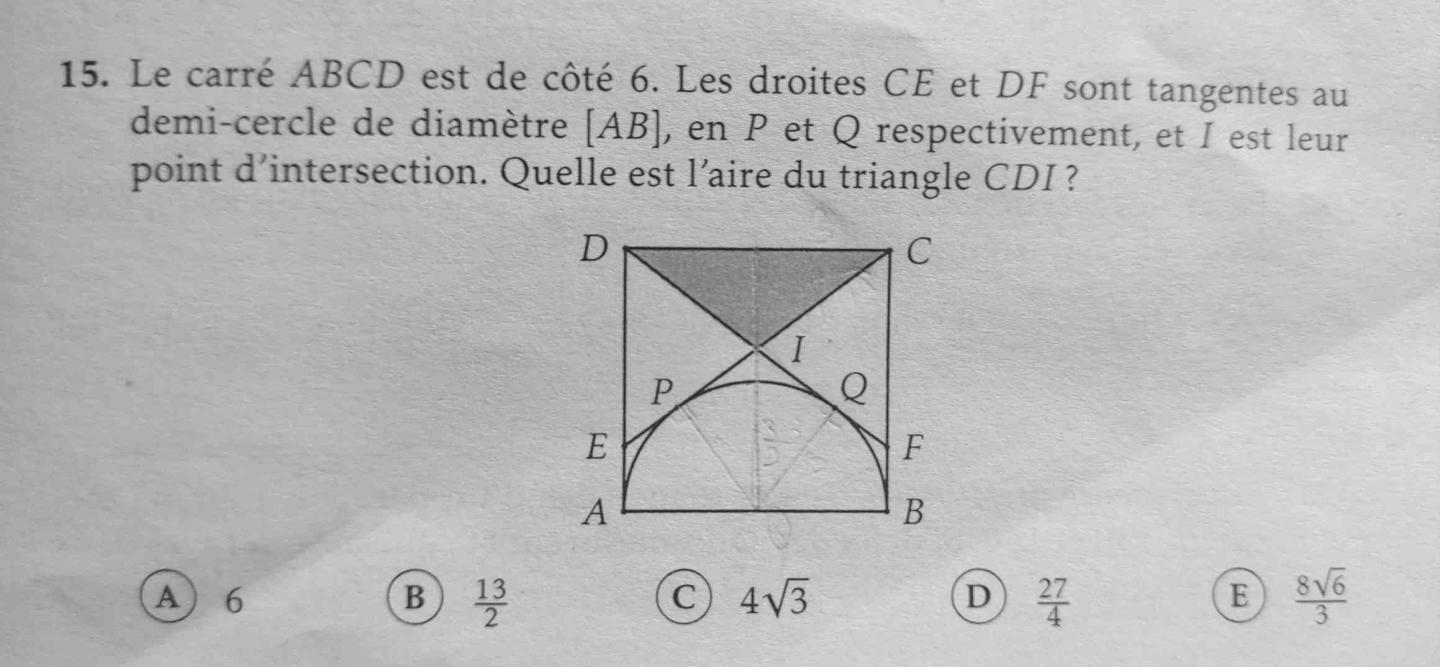
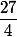Bon plus simple, juste avec Pythagore...

Soit M le milieu de [AB] et N celui de [DC]
les triangles DNI et IMQ sont isométriques (car angles égaux et MQ=DN=3)

Si on pose NI=h et DI=y on a y²=h²+9 (Pythagore)
et d'autre part h+y=6 (car DI=IM) d'où y = 6-h

On obtient une équation en h : (6-h)²=h²+9 ou 27=12h

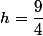
donc et l'aire grisée vaut

[Thiéfaine]

merci haha

[Rdvn]

Belle solution !