Triangle à côtés entiers et rayon du cercle inscrit

[Zweig]

Salut,

i) Le rayon du cercle inscrit à un triangle ABC, à côtés entiers, est 1. Montrer que ce triangle est rectangle.

ii) Montrer que si les côtés d'un triangle rectangle sont entiers, alors le rayon de son cercle inscrit l'est aussi.

[Imod]

Salut !

Pour i), je ne suis pas allé au bout mais en notant les côtés du triangle , l'aire et le demi-périmètre on a : . En posant . Reste à montrer que (1;2;3) ou l'une de ses permutations est l'unique solution pour obtenir (a;b;c)=(3;4;5) et conclure .

Imod

[Zweig]

J'ai fait exactement pareil :happy2: Enfin, j'ai utilisé la relation 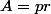, qui se rammène à 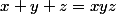. Après résoudre 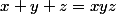dans les naturels n'a rien de difficile :

Puisque l'équation est symétrique en ses variables, on peut toujours supposer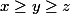 , alors 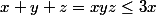, c'est-à-dire, 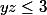. On vérifit que parmi les différents couples possibles, seul convient. On en tire alors 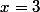. Il nous reste alors le système suivant à résoudre :





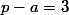
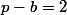
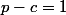
qui fournit le triplet . On conclut via Pythagore.

[lapras]

Pour le i), ca se torche avec héron !
en effet, l'aire du triangle est
A = r*(a+b+c)/2 avec r le rayon du cercle inscrit. (on le voit en découpant le triangle en 3 triangles et en sommant les aires)
r = 1 <=>
4*A² = (a+b+c)²
en changeant les variables :
x = p-a
y = p-b
z = p-c
On a x+y+z = 3p-(a+b+c) = 3p-2p = p
d'où
4*(x+y+z)*x*y*z = 4*(x+y+z)² <=> x+y+z = xyz
x(yz-1) = y+z
ce qui se torche par inégalité (on a immédiatement x = 1) et donc yz = y+z+1 qui admet, sauf erreur, (toujours par inégalité), comme seule solution (2,3)
d'où
(x,y,z) = (1,2,3) et permutations
On entire (a,b,c) = (3,4,5) et permutations (sauf erreur)
ce qui correspond bien a un triplet de pythagore : 3²+4² = 5² :happy2:

[lapras]

Ah j'ai été trop long pour taper !! :cry: Grillé...

[lapras]

Le ii) est aussi facile:
On a : A = a*b/2
d'où :
r = (a*b)/(a+b+c)
or a = p²-q²
b = 2pq
c = p²+q² (car a²+b² = c²)
on trouve alors immédiatement que r est entier (factorisation p²-q² = (p-q)(p+q)) :++: