Formule pour rapport corde,arc
17 messages
- Page 1 sur 1
formule pour rapport corde,arc
Bonjour,
Je suis nouveau dans ce forum pour la simple raison qu'il ne m'arrive pas souvent d'avoir besoin des mathematiques autre que la trigonometrie et quelques autres theoremes celebres. Je fais enormement de dessin technique pour mon travail et il m'arrive parfois d'utiliser les maths pour trouver des developpements. Les raisons etant la precision et la rapidite compare au trait. Aujourd'hui, je suis devant un probleme auquel personne de mon entourage ne peut repondre.
Il s'agit de:
2 cercles ayant le meme centre. r et R inconnus (r petit cercle, R grand cercle)
2 rayons formant un secteur commun aux 2 cercles. angle d'ouverture inconnu
je connais la longueur de l'arc de cercle sur le petit cercle
Je connais la longueur de la corde sur le grand cercle
je connais la longueur de la mediane qui part perpendiculairement du centre de la corde jusqu'au centre de l'arc de cercle
Question: comment calculer la longueur d'un des deux rayon?
si vous avez besoin d'un dessin parce-que mes expliquations ne sont pas assez claires, je peux aranger ca.
merci
Bruno
Je suis nouveau dans ce forum pour la simple raison qu'il ne m'arrive pas souvent d'avoir besoin des mathematiques autre que la trigonometrie et quelques autres theoremes celebres. Je fais enormement de dessin technique pour mon travail et il m'arrive parfois d'utiliser les maths pour trouver des developpements. Les raisons etant la precision et la rapidite compare au trait. Aujourd'hui, je suis devant un probleme auquel personne de mon entourage ne peut repondre.
Il s'agit de:
2 cercles ayant le meme centre. r et R inconnus (r petit cercle, R grand cercle)
2 rayons formant un secteur commun aux 2 cercles. angle d'ouverture inconnu
je connais la longueur de l'arc de cercle sur le petit cercle
Je connais la longueur de la corde sur le grand cercle
je connais la longueur de la mediane qui part perpendiculairement du centre de la corde jusqu'au centre de l'arc de cercle
Question: comment calculer la longueur d'un des deux rayon?
si vous avez besoin d'un dessin parce-que mes expliquations ne sont pas assez claires, je peux aranger ca.
merci
Bruno
Bonjour
Il s'agit sans doute de la flèche. Prolonge-la jusqu'au centre des cercles. Sa longueur (connue) est la différence entre le rayon R (inconnu) et la hauteur du triangle isocèle qui a le centre comme sommet principal (hauteur à calculer en fonction du rayon R et de la longueur de la corde (connue) grâce au théorème de Pythagore) : la seule inconnue restante est R.je connais la longueur de la mediane qui part perpendiculairement du centre de la corde jusqu'au centre de l'arc de cercle
bonjour rene38
Merci de t'interesser a mon probleme, mais je ne vois pas de quel triangle isocele tu parles. Je connais en effet la corde du grand cercle et la distance qui la separe de l'arc de cercle sur le petit cercle, mais je ne connais pas le rayon du petit cercle. donc je ne connais pas la corde du petit cercle. rien ne me permet de calculer un triangle si je ne connais que la base.
Bruno
Merci de t'interesser a mon probleme, mais je ne vois pas de quel triangle isocele tu parles. Je connais en effet la corde du grand cercle et la distance qui la separe de l'arc de cercle sur le petit cercle, mais je ne connais pas le rayon du petit cercle. donc je ne connais pas la corde du petit cercle. rien ne me permet de calculer un triangle si je ne connais que la base.
Bruno
Je viens de me relire et en meme temps viens de comprendre la ou tu aurais pu te tromper dans l'interpretation de mes donnees. Quand je dis du centre de la corde jusqu'au centre de l'arc de cercle, ca n'est pas le centre du cercle sur lequel se trouve cet arc de cercle mais bien le centre de l'arc de cercle. Donc cette mediane est en fait la distance entre la corde et l'arc de cercle. J'espere que c'est assez clair.
merci
Bruno
merci
Bruno

Voila ce que je comprends:
Tu connais la longueur jaune, bleue et verte. (je les appelles j, b et v)
J'appelle a, l'angle.
j/2=r(a/2)
a/2=j/2r
tan(a/2)=tan(j/2r)
mais,
donc (v+r)tan(j/2r)=b/2
(v+r)tan(j/2r)-b/2=0
reste plus qu'a trouver les 0 de cette fonction (fonction de r uniquement).
As tu des valeurs concrètes a proposer ?
Merci beaucoup pour cette reponse rapide Flodelarab!!
Ton dessin est correcte.
Oui je peux te proposer des valeurs tel que:
j=62.8
b=150
v=180
quel rayon calcules tu avec cette formule? le grand ou le petit?
peux-tu aussi m'indiquer ou apparait le resultat de l'angle dans le calcul, si il apparait.
merci encore.
Ton dessin est correcte.
Oui je peux te proposer des valeurs tel que:
j=62.8
b=150
v=180
quel rayon calcules tu avec cette formule? le grand ou le petit?
peux-tu aussi m'indiquer ou apparait le resultat de l'angle dans le calcul, si il apparait.
merci encore.
Si le rayon r est très grand, comme ton j est fixe, l'angle va tendre vers 0. Il n'y a pas de solution.
Si ton r est petit, tu as une infinité de solutions.
Pkoi ?
car la fonction tangente est périodique.
Je ne peux te donner que le plus grand r possible:
8,92172
mais sache que tu pourrais aussi avoir:
4,7
3,1
2,3
...
cela te suffit-il ?
Si ton r est petit, tu as une infinité de solutions.
Pkoi ?
car la fonction tangente est périodique.
Je ne peux te donner que le plus grand r possible:
8,92172
mais sache que tu pourrais aussi avoir:
4,7
3,1
2,3
...
cela te suffit-il ?
Ce problème m'intrigue.
Car même si la réponse est juste, on trouve une réponse du a un artifice de calcul.
On trouve une infinité de solutions uniquement pasqu'on considère qu'un angle de 420° est pareil qu'un angle de 60° ... mais dans le réel, ça change rien.
le plus grand r donne l'angle le plus petit (donc celui avec une "vraie" signification)
J'aimerais bien savoir ce que tu en penses René38 ?
Car même si la réponse est juste, on trouve une réponse du a un artifice de calcul.
On trouve une infinité de solutions uniquement pasqu'on considère qu'un angle de 420° est pareil qu'un angle de 60° ... mais dans le réel, ça change rien.
le plus grand r donne l'angle le plus petit (donc celui avec une "vraie" signification)
J'aimerais bien savoir ce que tu en penses René38 ?
brunojohanna a écrit:ce que je peux faire, c'est trouver le resultat par desssin, chose facile pour moi. Je vous ferais part ensuite des resultats approximatifs (imprecision du trait et de la prise de mesure) pour que vous puissiez savoir si vos calculs sont loin du compte (donc faux) ou pas (donc peut etre bon).
Je certifie à 100% l'infinité des solutions
Je certifie à 100% 8,92172
Les autres valeurs sont indicatives car g eu la flemme de chercher les décimales.
Salut,
Je ne comprends pas comment tu peux avoir r=8.92172 quand v=180.
Est-ce le rayon du cercle sur lequel se trouve j ? ou bien le rayon du grand cercle qui serait donc impossible.
Autre chose, je n'ai pas encore fait le dessin, mais je sais que le rayon (meme du petit cercle) est bien superieur a 8.9...
Pour te donner un ordre d'idee, quand je fais ce type de dessin, le rapport entre les dimensions sont toujours a peu pres du meme ordre et le rayon du grand cercle est toujours bien superieur au double de v. Dans ce cas ca nous donnerait un rayon de plus de 360. C'est pourquoi 8.9... me dit que le calcul est faux. Moi meme, je serais incapable de trouver la solution par calcul et je comprend que le probleme n'est pas facile a resoudre, mais la seule chose que je puisse faire c'est t'indiquer si le resultat semble probable ou faux.
merci encore pour le travail deja effectue et j'espere ne pas t'avoir decourage pour que te puisses trouver reponse a cette colle qui maintenant me parait bien plus complique que ce que je pensais.
Je ne comprends pas comment tu peux avoir r=8.92172 quand v=180.
Est-ce le rayon du cercle sur lequel se trouve j ? ou bien le rayon du grand cercle qui serait donc impossible.
Autre chose, je n'ai pas encore fait le dessin, mais je sais que le rayon (meme du petit cercle) est bien superieur a 8.9...
Pour te donner un ordre d'idee, quand je fais ce type de dessin, le rapport entre les dimensions sont toujours a peu pres du meme ordre et le rayon du grand cercle est toujours bien superieur au double de v. Dans ce cas ca nous donnerait un rayon de plus de 360. C'est pourquoi 8.9... me dit que le calcul est faux. Moi meme, je serais incapable de trouver la solution par calcul et je comprend que le probleme n'est pas facile a resoudre, mais la seule chose que je puisse faire c'est t'indiquer si le resultat semble probable ou faux.
merci encore pour le travail deja effectue et j'espere ne pas t'avoir decourage pour que te puisses trouver reponse a cette colle qui maintenant me parait bien plus complique que ce que je pensais.
brunojohanna a écrit:Salut,
Je ne comprends pas comment tu peux avoir r=8.92172 quand v=180.
Est-ce le rayon du cercle sur lequel se trouve j ? ou bien le rayon du grand cercle qui serait donc impossible.
Autre chose, je n'ai pas encore fait le dessin, mais je sais que le rayon (meme du petit cercle) est bien superieur a 8.9...
Pour te donner un ordre d'idee, quand je fais ce type de dessin, le rapport entre les dimensions sont toujours a peu pres du meme ordre et le rayon du grand cercle est toujours bien superieur au double de v. Dans ce cas ca nous donnerait un rayon de plus de 360. C'est pourquoi 8.9... me dit que le calcul est faux. Moi meme, je serais incapable de trouver la solution par calcul et je comprend que le probleme n'est pas facile a resoudre, mais la seule chose que je puisse faire c'est t'indiquer si le resultat semble probable ou faux.
merci encore pour le travail deja effectue et j'espere ne pas t'avoir decourage pour que te puisses trouver reponse a cette colle qui maintenant me parait bien plus complique que ce que je pensais.
J'avais fait le meme raisonnement que toi.
r est le rayon du petit cercle et R le rayon du grand cercle.
J'ai bien conscience que ça a l'air un peu absurde. Moi non plus je ne suis pas satisfait de cette réponse. Mais g beau retourné le calcul dans tous les sens, ya apparemment pas de faute.
En tout cas, le calcul ne ment pas. Il y a donc une faute de raisonnement .... mais je vois pas.
f(r)=(v+r)tan(j/2r)-b/2
f est une fonction trop compliquée pour que je l'inverse. Donc je trace sa courbe et je regarde quand ça coupe l'axe des x (pour trouver le zéro).
Je suis formel. il n'y a plus de valeur après 9 ....
felicitations
Felicitations,
tu as trouve, c'est bien ca. 133.87
j'ai verifie par dessin sur mon logiciel cad pour avoir des mesures ultra precises et c'etait parfait. Je te tire mon chapeau !!
mon probleme est maintenant de reproduire ce calcul. je relisais ta formule, et je ne vois pas comment l'utiliser avec ma calculatrice scientifique. Je possede une vieille casio fx 880p et je pense que ca devrait faire l'affaire mais comment est-ce que je dois proceder??
pourrais-tu m'ecrire les differentes etapes de calcul que tu utilisais pour trouver le resultat.
merci encore
tu as trouve, c'est bien ca. 133.87
j'ai verifie par dessin sur mon logiciel cad pour avoir des mesures ultra precises et c'etait parfait. Je te tire mon chapeau !!
mon probleme est maintenant de reproduire ce calcul. je relisais ta formule, et je ne vois pas comment l'utiliser avec ma calculatrice scientifique. Je possede une vieille casio fx 880p et je pense que ca devrait faire l'affaire mais comment est-ce que je dois proceder??
pourrais-tu m'ecrire les differentes etapes de calcul que tu utilisais pour trouver le resultat.
merci encore
Je ne comprends pas précisément ton besoin et tes ressources.
Comme tu l'as compris, on peut écrire une formule en fonction de r MAIS les r (valeurs du petit rayon) permettant d'annuler cette fonction sont en quantité infinie.
Pour qu'on se comprenne, voila une représentation graphique de cette fonction:

LE problème est que cette fonction est non inversible (selon moi). Donc la seule façon de trouver r est de tâtonner.
plusieurs solutions:
Explication de la dichotomie:
Comme on sait que la courbe va passer des positifs aux négatifs 1 fois et une seule, on va pouvoir resserrer l'intervalle de valeurs possibles autour de la vraie valeur.
Concrétement, tu choisis 2 bornes B1 et B2.
si f((B1+B2)/2) est positif alors B1 prend la valeur (B1+B2)/2
si f((B1+B2)/2) est négatif alors B2 prend la valeur (B1+B2)/2
Et on recommence...
Ton intervalle va etre réduit de moitié a chaque fois.
Quelle condition d'arret ? (obligatoire pour ton programme)
B2-B1\frac{j}{\pi}[/TEX]
Donc tu peux partir de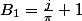 et B2 = 50000 par exemple.
et B2 = 50000 par exemple.
J'ai pris une valeur arbitraire et farfelue pour B2 mais suffisamment grande.
Et moi?
Moi g utilisé gnuplot, gratuit et téléchargeable, g tracé la courbe et g zoomé a mort sur le point d'intersection.
Est-ce clair ?
Est-ce utilisable ?
As tu encore besoin d'aide ?
Comme tu l'as compris, on peut écrire une formule en fonction de r MAIS les r (valeurs du petit rayon) permettant d'annuler cette fonction sont en quantité infinie.
Pour qu'on se comprenne, voila une représentation graphique de cette fonction:

LE problème est que cette fonction est non inversible (selon moi). Donc la seule façon de trouver r est de tâtonner.
plusieurs solutions:
- Si tu as une utilisation peu fréquente de ce calcul, et que tu as un ordi ou une calculette graphique, zoome à mort sur le point d'intersection entre la courbe rouge et l'axe vert (jusqu'a obtenir la précision voulue).
- Si tu as une utilisation plus fréquente (pour faire des comparaisons de valeurs par exemple), il faut utiliser une méthode plus systématique comme la méthode de Newton-Raphson ou par dichotomie (comme on se moque de l'efficacité de l'algorithme, je vais t'expliquer la dichotomie).
- Avec un ordi, avec un tableur classique
- Avec ta calculette. (Tu sais la programmer en basic ?)
Explication de la dichotomie:
Comme on sait que la courbe va passer des positifs aux négatifs 1 fois et une seule, on va pouvoir resserrer l'intervalle de valeurs possibles autour de la vraie valeur.
Concrétement, tu choisis 2 bornes B1 et B2.
si f((B1+B2)/2) est positif alors B1 prend la valeur (B1+B2)/2
si f((B1+B2)/2) est négatif alors B2 prend la valeur (B1+B2)/2
Et on recommence...
Ton intervalle va etre réduit de moitié a chaque fois.
Quelle condition d'arret ? (obligatoire pour ton programme)
B2-B1\frac{j}{\pi}[/TEX]
Donc tu peux partir de
J'ai pris une valeur arbitraire et farfelue pour B2 mais suffisamment grande.
Et moi?
Moi g utilisé gnuplot, gratuit et téléchargeable, g tracé la courbe et g zoomé a mort sur le point d'intersection.
Est-ce clair ?
Est-ce utilisable ?
As tu encore besoin d'aide ?
Re: formule pour rapport corde,arc
la trigonométrie c'est intéressant (a2+b2=hypoténuse au carré (Merci Pythagore, Fermat, Pascal, Trrotski, Jésus, mos et momo ) mais il ne faut pas oublier que 1+1=3 en imaginaire pur. Alors ne t'inquiètes pas, tu trouvera tout jours des internotes sympa ici. 

 : je suis incognito !
: je suis incognito !


 : je suis incognito !
: je suis incognito !
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

