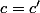Fonctions du second degré(et rien d'autre)

[yavlory]

Bonjour
fonctions du second degré(et rien d'autre)

un super joli problème de géométrie du niveau seconde
aucun pré-requis autre que les fonctions et équations du second degré vues en cours

j'écrirai la démonstration de ce problème demain
Elle tient en vingt lignes
______________
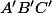
Soient et deux triangles
on notera
, ,
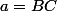
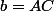
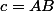
l'angle géométrique issu de du triangle
l'angle géométrique issu de du triangle
l'angle géométrique issu de du triangle
le rayon du cercle circonscrit du triangle
l'aire du triangle
, ,
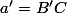
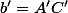
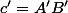
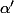
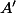
l'angle géométrique issu de du triangle
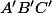
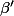
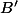
l'angle géométrique issu de du triangle
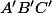
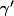
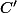
l'angle géométrique issu de du triangle
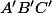
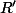
le rayon du cercle circonscrit du triangle
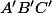
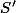
l'aire du triangle

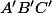Démontrer que pour ces deux triangles et à isométrie près que
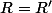
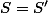
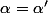
Si et et et
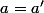
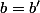
Alors et

[Ben314]

Salut,
(1) On trace un cercle de rayon R.
(2) VU que l'angle (BAC) vaut alpha, c'est que l'angle (BOC) vaut 2.alpha (*) ce qui permet de tracer B et C (à rotation prés, mais on s'en fout vu qu'on est à isométrie prés)
(2') Ça sert évidement à rien de connaître la longueur a=BC vu qu'on vient de voir qu'avec alpha et R on peut tracer [BC] à isométrie près.
(3) On ne garde du cercle que l'arc BC correspondant aux A tels que l'angle (BAC) vaille alpha (*).
(4) Si on veut en plus que l'aire du triangle ABC soit égale à un S donné, ça signifie que A doit être situé sur une certaine droite D parallèle à (BC) et il n'y a (au mieux) que deux solutions qui en fait sont symétrique l'une de l'autre par rapport à la médiatrice de [BC] (donc une seule solution à isométrie près).

Et ça permet en plus de voir que, pour alpha et R fixé, il y a un maximum possible pour l'aire qui est obtenu lorsque le triangle est isocèle en A.

(*) Vu en 3em sauf erreur.

[yavlory]

Bonjour Ben
avec ma démo (que je posterai demain)ça donne l'occasion d'utiliser une fonction et une équation du second degré
c'est joli et original et utile pour la classe de seconde

[Ben314]

avec ma démo (que je posterai demain)ça donne l'occasion d'utiliser une fonction et une équation du second degré
c'est joli et original et utile pour la classe de seconde

C'est tout à fait vrai que la notion de "joli et original" est forcément relative vu que, perso, d'utiliser du calcul bourrin pour résoudre un truc qui se fait très bien de tête en visualisant juste un dessin, ben j'aurais plutôt tendance à trouver ça "moche et stupide".

[yavlory]

stupide oui sauf dans le cadre d'un cours sur les fonctions et d'un autre cours sur les équations du second degré
Ben314 attends demain, tu sera bluffé(je laisse le suspens)

[Ben314]

stupide oui sauf dans le cadre d'un cours sur les fonctions et d'un autre cours sur les équations du second degré
Ben314 attends demain, tu sera bluffé(je laisse le suspens)

NON : ça je peut pas laisser passer.
Si dans un cours sur la notion XXX, tout ce que tu as à raconter comme "applications" de la notion en question, c'est de s'en servir pour des problèmes qu'on sait déjà résoudre par de moyens bien plus simples et direct, c'est que tu prend vraiment les élèves à qui tu t'adresse pour des débiles mentaux complets (et/ou que tu les incite à le devenir...)

Une nouvelle notion, ça sert évidement soit à résoudre de nouveau problèmes, soit à résoudre plus vite et plus simplement des problèmes qu'on savait déjà résoudre précédemment.

[yavlory]

Demain mon ami tu verra qu'un aveugle le fait sans visualisation
en clair sans savoir c'est quoi une figure
bonne nuit mon ami

[yavlory]

Mon ami Ben 314
En attendant ma démonstration(que je posterai aujourd'hui comme je l'ai promis) j'espère que ce lien là->https://www.maths-forum.com/detente/possibilite-devenir-intellect-complet-t193507.html#p1284761
te fera changer d'optique
car il vaut toujours mieux changer d'optique avant de voir plutôt qu'après, ce que donne l'initiative de travailler pour l'exécution de l'intelligence complète qui oeuvre derrière

[yavlory]

qui se fait très bien de tête en visualisant juste un dessin, ben j'aurais plutôt tendance à trouver ça "moche et stupide".

surveille ta langue stp
tu parles comme une pute là

[Ben314]

surveille ta langue stp
tu parles comme une pute là

J'ai toujours considéré qu'il valait 100 fois mieux dire des choses intelligentes avec une "langue de pute" (*) que d'énorme conneries dans un langage châtié (et dieu sait qu'une telle réflexion, je ne me la suis pas fait qu'en math...)

(*) Et je te laisse l'entière responsabilité de l'utilisation du mot "pute" dans un tel contexte.

[Lostounet]

surveille ta langue stp
tu parles comme une pute là

Votre compte a été désactivé par l'équipe de modération.