Equation de la trajectoire en fonction de t
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mar 2012, 19:43
par Zweig » 08 Mar 2012, 19:43
Salut,
Soit
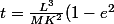^{\displaystyle -\frac{3}{2}}(\phi-e\sin\,\phi)+t_0)
J'aimerai exprimer

en fonction de

et des constantes ... Comment faire ? Le calcul ne m'a pas l'air trivial (mais je sais que c'est possible). En fait, je ne cherche pas vraiment à le faire à la main, c'est même plutôt conseillé de le faire via un logiciel de calcul formel si c'est possible.
Merci d'avance.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 08 Mar 2012, 20:15
par Doraki » 08 Mar 2012, 20:15
en fait tu cherches à exprimer la réciproque de la fonction ;) -> ;) - e*sin ;) où e est une constante ? (avec |e|<1 ?)
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mar 2012, 20:22
par Zweig » 08 Mar 2012, 20:22
C'est un problème de méca céleste. Je cherche à exprimer la position d'une planète (soumise à l'attraction du Soleil seulement) en fonction du temps seulement. A l'aide des lois de Képler toussa, j'ai les coordonnées des positions de la forme
, \theta))
. Je voudrai maintenant exprimer

en fonction de t (et d'autres diverses constantes) pour avoir les positions en fonction du temps seulement.
Pour ça, il me manque plus qu'à obtenir, via l'équation (équation du temps de Képler) ci-dessus,
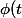)
, mais je ne vois pas comment isoler

(à cause du sinus)
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mar 2012, 20:32
par Zweig » 08 Mar 2012, 20:32
Doraki a écrit:en fait tu cherches à exprimer la réciproque de la fonction

->

- e*sin

où e est une constante ? (avec |e|<1 ?)
Oui :mur:

-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 08 Mar 2012, 21:02
par Doraki » 08 Mar 2012, 21:02
ben je doute fort qu'il y ait une expression simplifiée.
la réciproque est de la forme y + f(y) avec f périodique.
Ptetre que ça sert à quelquechose d'expliciter f comme série de Fourier.
Si je me souviens bien la trajectoire est une ellipse et la planète tourne de sorte que l'aire balayée par le segment entre le planète et je sais plus quel point est une constante.
Rien ne présage à ce que la vitesse angulaire (et donc ;)(t)) soit très très simple.
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 08 Mar 2012, 21:03
par Mathusalem » 08 Mar 2012, 21:03
Zweig a écrit:Salut,
Soit
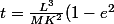^{\displaystyle -\frac{3}{2}}(\phi-e\sin\,\phi)+t_0)
J'aimerai exprimer

en fonction de

et des constantes ... Comment faire ? Le calcul ne m'a pas l'air trivial (mais je sais que c'est possible). En fait, je ne cherche pas vraiment à le faire à la main, c'est même plutôt conseillé de le faire via un logiciel de calcul formel si c'est possible.
Merci d'avance.
C'est la solution de l'équation de Newton avec Kepler dedans pour le mouvement d'une planète autour du soleil ? Si c'est le cas, tu peux montrer avec de la mécanique analytique qu'il n'est pas possible d'obtenir une expression de phi(t) (Impossibilité de résoudre les équations de Hamilton-Jacobi car pas assez de constantes du mouvement, si ça t'intéresse). Pour autant que phi repère l'angle sous le rayon Soleil-Planete.
Autrement, à l'instinct je dirais que puisques tu as à faire à une équation transcendentale (? quand y a du linéaire et du trigo ?), je vois pas comment tu vas pouvoir isoler phi qui apparaît dans un sinus et aussi dans un terme linéaire.
EDIT: Je viens de voir tous les posts. Je confirme, tu vas pas pouvoir trouver phi(t).
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 08 Mar 2012, 21:26
par Nightmare » 08 Mar 2012, 21:26
Hello,
le "peut être calculée" ne veut pas dire "peut s'exprimer comme somme finie de fonctions élémentaires".
On peut effectivement inverser ta fonction à l'aide de série entière ou de Fourier comme Doraki l'indique mais on en obtiendra pas d'expression usuelle.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mar 2012, 21:35
par Zweig » 08 Mar 2012, 21:35
D'accord, car une (bonne) approximation m'est tout aussi suffisante en fait :lol3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 08 Mar 2012, 21:36
par Nightmare » 08 Mar 2012, 21:36
Oui, à vrai dire, c'est en terme de calculabilité même plus suffisant qu'une grosse expression avec des log et cie dont on ne peut de toute manière calculer les valeurs qu'en faisant là aussi des approximations.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mar 2012, 21:39
par Zweig » 08 Mar 2012, 21:39
Du coup, quel était le calcul que l'auteur du PDF avait en tête ?
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 09 Mar 2012, 14:38
par Mathusalem » 09 Mar 2012, 14:38
Zweig a écrit:Du coup, quel était le calcul que l'auteur du PDF avait en tête ?
Je pense une resolution numerique de l'equation pour un temps t fixe. Ensuite remplacer dans l'equation reliant r a phi.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 09 Mar 2012, 14:47
par Zweig » 09 Mar 2012, 14:47
En effet, pas bête ... Merci !
-
jmsm56
- Messages: 1
- Enregistré le: 09 Mar 2012, 18:23
-
 par jmsm56 » 09 Mar 2012, 18:41
par jmsm56 » 09 Mar 2012, 18:41
Zweig a écrit:Salut,
Soit
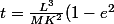^{\displaystyle -\frac{3}{2}}(\phi-e\sin\,\phi)+t_0)
J'aimerai exprimer

en fonction de

et des constantes ... Comment faire ? Le calcul ne m'a pas l'air trivial (mais je sais que c'est possible). En fait, je ne cherche pas vraiment à le faire à la main, c'est même plutôt conseillé de le faire via un logiciel de calcul formel si c'est possible.
Merci d'avance.
Bonjour.
C'est la classique équation du mouvement des planètes.
Le Traité de mécanique rationnelle de Paul Appell (l'édition que j'ai date de 1902...) consacre 5 pages à cette question pas vraiment simple. Pas de réponse par une formule explicite finie ; 3 méthodes sont proposées :
-- approximations successives : on prend les valeurs de t une à une...
-- série de Lagrange : développement en puissances de l'excentricité e, mais il faut e < 0,662743... pour que la série converge.
-- série de Fourier, utilisant les fonctions de Bessel (convergeant pour tout e )
Je pense donc qu'un logiciel de calcul formel va sécher ; l'une ou l'autre méthode d'approximation numérique est programmable, bien sûr.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 09 Mar 2012, 19:23
par Zweig » 09 Mar 2012, 19:23
Merci pour ces précisions !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
en fonction de
et des constantes ... Comment faire ? Le calcul ne m'a pas l'air trivial (mais je sais que c'est possible). En fait, je ne cherche pas vraiment à le faire à la main, c'est même plutôt conseillé de le faire via un logiciel de calcul formel si c'est possible.
en fonction de
et des constantes ... Comment faire ? Le calcul ne m'a pas l'air trivial (mais je sais que c'est possible). En fait, je ne cherche pas vraiment à le faire à la main, c'est même plutôt conseillé de le faire via un logiciel de calcul formel si c'est possible.