[Défi] Equation "non standard"
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 16:50
par Zweig » 17 Aoû 2009, 16:50
Salut,
Un petit défi ouvert à tous les lycéens (à part lapras et autres tôrcheurs d'exercices difficiles :we:) . Déterminer tous les triplets de réels
)
vérifiant l'équation suivante :
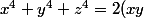^2 + 2(xz)^2 + 2(yz)^2)
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2009, 17:10
par egan » 17 Aoû 2009, 17:10
En considérant y et z comme des paramètres, on arrive sur une équation du second degrès en faisant un changement de variable. Après doit y avoir des conditions mais ça me semblerait être un bon début.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 17:24
par Zweig » 17 Aoû 2009, 17:24
Cette technique peut marcher dans le cas où les variables sont des entiers ... Je n'ai pas expérimenté ici, mais je doute qu'on arrive à quelque chose ...
-
Black Jack
 par Black Jack » 17 Aoû 2009, 17:45
par Black Jack » 17 Aoû 2009, 17:45
Salut,
J'ai trouvé... mais je ne dis rien, il y a trop longtemps que je ne suis plus lycéen.
:zen:
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2009, 17:48
par egan » 17 Aoû 2009, 17:48
Zweig a écrit:Cette technique peut marcher dans le cas où les variables sont des entiers ... Je n'ai pas expérimenté ici, mais je doute qu'on arrive à quelque chose ...
Pourquoi des entiers ?
Quand on résout un système de deux équations à trois inconnus dans R, on considère un des inconnus comme un paramètre. C'est le même principe ici.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 17:54
par Zweig » 17 Aoû 2009, 17:54
Ce n'est pas un système ici ... Ici, le discriminant sera exprimé en fonction de 2 variables, et après ?
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2009, 18:06
par egan » 17 Aoû 2009, 18:06
Ah oui j'avais pas pensé à ça. Déterminer le signe du discriminant en fonction de deux variables sera pas aisé. Quoique ça dépend de la tête qu'aura son expression.
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2009, 18:12
par egan » 17 Aoû 2009, 18:12
Remarque même si le discriminant à une mauvaise tête, avec les outils qui permettent d'étudier les fonctions à deux variables, ça doit être faisable non ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 18:14
par Zweig » 17 Aoû 2009, 18:14
Bah, depuis quand on étudie les fonctions à deux variables au Lycée ? Pas besoin de chercher compliqué ... Un indice : on ramène le membre de droite à gauche, et on essaye de factoriser ...
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2009, 18:18
par egan » 17 Aoû 2009, 18:18
Oui c'est vrai que c'est pas un outils du lycée mais je disais ça dans le cas où ça aurait été pas cool sur l'expression du discriminant.
D'ailleurs, je l'ai calculé, si je me suis pas trompé, il est très gentil:

-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2009, 18:24
par egan » 17 Aoû 2009, 18:24
Une des solutions est
}=)
non ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 18:25
par Zweig » 17 Aoû 2009, 18:25
Ok j'ai rien dit alors. En effet, ça permet donc de factoriser très facilement si on connaît bien son cours sur les polynômes ...
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 18:30
par Zweig » 17 Aoû 2009, 18:30
Il y'a 4 couples solutions qui sont
 = (u+v, u, v),\, (-u-v, u, v),\, (u-v, u, v),\, (v-u, u, v))
avec
 \in\mathbb{R}^2)
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2009, 18:31
par egan » 17 Aoû 2009, 18:31
Oui ça se fait mais c'est assez long. Il y aura les trois cas où le discriminant est nul et celui où il est strictement positif. En plus, comme les solutions trouvées sont des carés, il faut s'assurer qu'elles soient positives.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 18:33
par Zweig » 17 Aoû 2009, 18:33
Euh non, c'est très direct à partir du discriminant ...
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2009, 18:37
par egan » 17 Aoû 2009, 18:37
Tu trouves ça normalement:
^2=y^2+z^2+2abs(zy))
^2=y^2+z^2-2abs(zy))
Il faut s'assurer que
^2=y^2+z^2-2abs(zy))
est positif.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 18:39
par Zweig » 17 Aoû 2009, 18:39
C'quoi "abs" ? Il manque l'exposant. Oui donc tu remarques des identités remarquables, ce qui te permet d'exprimer x en fonction de y et z et de conclure (voir mon message plus haut).
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 17 Aoû 2009, 18:42
par Jack the ripper » 17 Aoû 2009, 18:42
J'ai la même chose qu'egan je pense x1 et x2 positifs car ce sont des carrés
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 17 Aoû 2009, 18:42
par egan » 17 Aoû 2009, 18:42
C'est valeur absolue. Ou est-ce qu'il manque un exposant ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Aoû 2009, 18:46
par Zweig » 17 Aoû 2009, 18:46
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
) vérifiant l'équation suivante :
vérifiant l'équation suivante :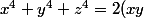^2 + 2(xz)^2 + 2(yz)^2)
