De dimension son cardinal

[Nightmare]

Salut à tous !

Un joli exercice d'algèbre faisable au lycée :

E désigne la partie entière.

1) Montrer que pour tout réel, existe et est finie. On appelle cette limite.

2) Soit , montrer que s'il existe tels que alors les sont tous nuls.

3) Justification du titre?

Bon courage

:happy3:

[Nightmare]

Pour la question 2) qui est la principale du problème, voici un premier "lemme" à démontrer pour démarrer :

[COLOR="white"]Montrer que pour a fixé tel que 0 < a < min(xi), on va pouvoir trouver un intervalle de longueur a qui ne contient aucun kxi avec k entier et montrer qu'on peut trouver un tel intervalle aussi loin de 0 qu'on veut.[/Color]

[Anonyme]

Salut Nighmare !

Pour la 1) pas de problème:

La suite est croissante montrons qu'elle est majorée,
En effet donc avec
(Bernoulli)

On a que . En prenant on trouve que or ,
donc ,



qui converge bien entendu (somme des termes d'une suite géométrique de raison <1)

J'ai pas encore lu la 2) est ce faisable sans avoir lu ton lemme ?

Edit : c'est quoi cette erreur Latex
Edit 2: Apparement il ne faut pas commencer une commende Latex par un -

[Nightmare]

Personnellement (mais je ne suis pas le meilleur exemple) je n'ai pas su comment démarrer, et même avec le lemme donné, j'ai bloqué un petit moment avant d'arriver à quelque chose de convainquant. Cela dit, tous les outils nécessaires sont de niveau lycée.

[Anonyme]

Il faudrait que les x_i soient différents non ? Parce que sinon je prend 2k termes égaux et je choisis les alternativement 1 et -1 et le tour est joué.

[Nightmare]

Oui, bien entendu, on les prend distincts !

[Anonyme]

Ne suffit-il pas que l'un d'entre eux uniquement soit distinct des autres ?

[Nightmare]

Cela revient au même. n est quelconque, donc on peut (et doit) considérer des familles de n'importe quel cardinal. Ici, considérer une famille a n éléments avec n-1 égaux et un différent revient à considérer une famille à 2 éléments distincts.

[Anonyme]

Je pense avoir une solution pas tres rigoureuse pour l'instant mais assez intuitive et imagé. Elle consiste a regarder la partie décimale d'un nombre a partir d'un certain rang.

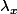
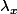
Deja on peut remarquer que tous les nombres en question sont de la formes 0,1001000010000000001 c'est a dire des 1 espacée par un nombre avec une suite croissante non majorée. C'est a dire que pour un nombre donnée on peut trouver un rang a partir duquel les "1" sont espacés autant que l'on veut. Soit le rand a partir duquel les "1" de l’écriture décimale de sont espaces de .

Un autre lemme : si et

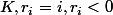En posant on a


Les nombres et sont égaux il ont même partie décimale.

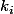
Je peux supposer quitte a changer l'ordre de que ceux si sont dans un ordre croissant.

En fait l’idée c'est d’examiner les écritures décimales de ces nombres a partir d'un certain assez grand pour montrer qu'elle ne sont pas égales. Il s'agit de chercher un rang a partir duquel soit de la forme abcde000abcde00000000abcde000000000000000 (vous avez compris l’idée je suppose).
Le 1er lemme nous assure que ce rang quelque soit la longueur du nombre.

Aussi ce rang doit vérifier la propriété suivante: doit être de la forme (a partir d'un certain rang bien sur) 00abcde0000000wxyz00000000000000abcde00000000. C'est a dire que l'addition se fait assez simplement sans que les deux nombres puissent interférer.
C'est l’idée sous-jacente du 2eme lemme en prenant n assez grand cela nous garanti que les termes de la sommes ne vont pas "interferer" entre eux.

En prenant un rang qui satisfait ces deux conditions on peut déduire qu' a partir de r l’écriture décimale de est différente de l’écriture décimale de ce qui conclu.

Je sens déjà les critiques arriver mais bon je vous avais prévenu c'est tout sauf rigoureux :ptdr:

[Doraki]

J'vois pas le rapport entre le lemme 2 et "à partir d'un certain rang, l'addition se fait assez simplement sans que les deux nombres puissent interférer."

[Anonyme]

En effet c'est pas suffisant :mur: J'avais pris un cas ou sa fonctionnait et il semble que celui ci soit très particulier. Je vais y réfléchir (même si je doute que ça aboutisse a quelque chose ) , il est peut être plus judicieux de travailler sur une séquence limitée de la partie décimale et pas de la considerer a partir d'un certain rang.

[Doraki]

Oui, montrer que tout se passe bien partout à partir d'un certain rang est déraisonnable (si ça se trouve c'est faux).
Trouver une fenêtre où on voit que dans un nombre un peut lire un ri et dans l'autre nombre c'est que des 0, c'est plus vraisemblable.

T'as juste à expliquer comment tu peux trouver une telle fenêtre avec tes lemmes.

[Anonyme]

T'as juste à expliquer comment tu peux trouver une telle fenêtre avec tes lemmes.

Justement l'explication que j'avais n'est pas valide même pour une séquence limitée faudra que je cherche une nouvelle avec peut être de nouveaux lemmes. En te lisant j'ai eu l'impression que es arrive a faire découler le résultat de ces lemmes est ce cas ?

[Doraki]

Ton 2ème lemme est bien mais pourrait être tourné de manière un peu plus pragmatique en termes de "telle occurence de 1 dans ;)xj gêne ou pas telle occurence de 1 dans ;)xi" (bien sur faut préciser ce que veut dire "gêner")

Mais bon déjà, faut que j'regarde le lemme de nightmare, j'ai l'impression que les xi du lemme = les log(xi) du problème alors c'était un peu fourbe son truc.

[Nightmare]

Mais bon déjà, faut que j'regarde le lemme de nightmare, j'ai l'impression que les xi du lemme = les log(xi) du problème alors c'était un peu fourbe son truc.

c'est bien ça !

[Anonyme]

Je laisse tomber ma demo pour le moment elle se base trop sur l'intuition je trouve et j'arrive pas a la corriger. J'ai très bien compris ce que voulais dire Doraki par le "1" qui dérange ou qui ne dérange pas et c’était sur cette idée que je me suis basée en premier mais j'arrive pas a traduire formellement cette idée.

Je vais regarder du coté de l'indice de Nightmare.