Cardinal maximal

[miikou]

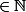
soit n \{0}
on considère A={1,2..... n} et B un sous ensemble de A tq ne soit pas un carré parfait.
Quel est le cardinal maximal de B ( en fonction de n biensur .. )

nb : i et j peuvent etre égaux

[lapras]

Voudrais-tu dire :

[miikou]

oui c'est bien ca ;)

[miikou]

Au fait bonne chance hahaha :D

[miikou]

trop difficile peut etre ?

[lapras]

Pas évident.
Déja
Peut être peut on démontrer que

[acoustica]

Au fait bonne chance hahaha

Qu'est ce que tu entends par là? C'est un problème que personne n'a résolu?
Parce que franchement, j'ai aucune idée de comment attaquer le problème... :mur:

[Clembou]

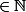
soit n \{0}
on considère A={1,2..... n} et B un sous ensemble de A tq ne soit pas un carré parfait.
Quel est le cardinal maximal de B ( en fonction de n biensur .. )

nb : i et j peuvent etre égaux

Peut être prendre chaque carré parfait. Le décomposer en somme de deux éléments et selon voir ce qu'il faut éliminer dans

[miikou]

si le probleme admet bien une solution, mais elle n'est pas evidente.
En tt cas bravo a lapras la minoration qu'il donne est exacte ;)

[acoustica]

comment on l'obtient cette minoration?

[miikou]

je ne sais pas comment il l'a obtenue mais je connais le card de B en fonction de n, et en effet il verifie bien cette inequation ..

[miikou]

petit up ;)